突然ですが、皆さんは「数学」が好きですか？　「数学」と聞くと、どんなことを思い浮かべますか？　「ひたすら計算をする」「とにかく公式を覚える」様々な思いがあることでしょう。今日は、そんな数学に対する気持ちを一新してみませんか。

中学数学でおなじみの「ピタゴラスの定理」

　今日は、「ピタゴラスの定理」を使って少し遊んでみたいと思います。「ピタゴラスの定理」とは、「直角三角形の直角をはさむ2辺の2乗の和は斜辺の2乗の和に等しい」というものです。つまり、「角Cを直角とし直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、（aの2乗）＋（bの2乗）＝（cの2乗）」というものです。これは「三平方の定理」とも呼ばれています。古代エジプトでは、土地を直角に区画整理する際にこの技法が利用されたとも言われています。この定理が成り立つもので、一番親しみのあるものが「3：4：5」の直角三角形です。ここで、中学校の時の授業を思い出してみると、証明をしたり、計算練習をしたり、という記憶が蘇ってきます。「3：4：5」という比率も、とりあえず覚えていただけで、特に深い意味のあるものだとは考えもしませんでした。

　しかし、「（3の2乗）＋（4の2乗）＝（5の2乗）」というあまりにも綺麗な等式が成り立つ3数3、4、5は、この等式よりも綺麗な性質を持っているのです。

数学を体で感じてみよう！

　実は、同じ張力で張られた弦で、「ド・ファ・ラ」の音が鳴る弦の長さを測ってみると、なんとその長さの比は、弦の長さが短い順に「3：4：5」になっているのです！　数学では単に綺麗な等式が成り立っていただけなのに、音にしてみると綺麗な和音となる音を奏でることが出来るなんて、なんだか不思議な感じがしますね。
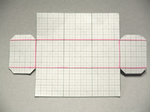
　実際に「ド・ファ・ラ」の音が鳴る弦を張って、その弦の長さを測ってみると楽しいものです。作り方の例を簡単にご紹介します。

1. 厚紙などで箱を作り、輪ゴムを1本取りつけます。
2. 輪ゴムを爪で摘まみながら、輪ゴムを弾き、「ド・ファ・ラ」の音が鳴る位置を探し、ペンで輪ゴムに印をつけます。（印をつけるのは、爪で摘まんでいたところです）
3. 箱の淵から、印をつけたところまでの長さ（輪ゴムを弾いた側の長さ）をそれぞれ測ります。「3：4：5」になっていることが確認できます。

　皆さんも実際に弦を張って音を奏で、数学を体で感じてみてはいかがでしょうか。

• 数学の授業で古代の土地区画を校庭に再現！(2009/5/23)
  http://www.meijitosho.co.jp/eduzine/kaigi/?id=20090181