- 協働的な学び
- 算数・数学
「『個別最適な学び』と『協働的な学び』を一体的に充実していくことが大切」と言われても、具体的に何をすればよいか想像がつかない方も多いのではないでしょうか。また、理論的なことを知ったとしても「それをどうやって教室でやればいいの?」と思う方もいらっしゃるのではないでしょうか。
今回は、3年生と一緒に、少しずつ「個別最適な学び」と「協働的な学び」を実現させていった学年当初の過程を述べていきます。まだまだ「『個別最適な学び』と『協働的な学び』を一体的に充実している姿」ではありませんし、道のりは遠いですが、どのように学習活動を積み重ねていけば、「個別最適な学び」や「協働的な学び」を実現していけるようになるのかを考えるきっかけにはなればと思います。
まず一斉授業で学習観と学び方を伝えていく
「個別最適な学び」と聞くと、どうしても個別学習が頭に浮かびます。しかし、個別学習を成立させるためには、一斉授業が重要です。
「個別最適な学び」と「協働的な学び」における一斉学習には、主に学習観と学び方を学ぶ場としての役割があります。学習観については第2回でも述べましたが、学び方を学ぶ場としての一斉授業の役割はとても大きいです。
下の写真は、3年生ではじめて行った一斉授業の板書の一部です。学習内容は、九九表のきまりを見つけるというものでした。
九九表の隣にいろいろな吹き出しが板書されていますが、これは、「どんなことに着目して、九九表のきまりを見つけたのか」という、問題を解くときの着眼点(数学的な見方)を言語化したものです。例えば、下から2つ目の「ななめで見る」という着眼点ですが、これは、「九九表の数がペアになっている」と発言をした子どもに、「どうやって九九表を見たら、そんなことに気づいたの?」と私が問うたときの答えを書いたものです。
次に、解き方の理由を考えることの大切さを伝えるために、「どうしてそうなるのか」ということを考えさせました。問題としては、先述の「九九表の数がペアになっている」というきまりの中から、「どうして左下にある14と右上にある14は同じ数になっているのか」ということを考えました。しかし、なかなか説明できる3年生はいません。結局、子どもだけでは説明ができなかったので、私から7×2のアレイ図を提示して「この図を使って説明できないかな?」と問いかけました。すると、何人かの子どもが「この図を動かせばいいのではないか」とつぶやき始め、それを黒板で共有していきました。実際に図をかいて説明すると、かけ算の交換法則がすっきりと理解しやすくなり、子どもからは「わかった!」という感嘆の声が上がりました。そして、他のところでも確かめる子どもの姿が見られるようになりました。
2単元目から個別学習を取り入れる
1単元目は全時間で一斉授業を行い、算数の学習観を共有した後、2単元目から個別学習を取り入れていきました。3年生の2単元目は、時間の計算です。ただし、単元の導入から個別学習にするのではなく、1時間目は一斉授業を行い、時間の計算の単元で重要な数学的な見方などを全体で押さえたうえで、2時間目以降に個別学習を行いました。個別学習といっても、いつでも、だれとでも関われることが認められた学習ということを忘れずに取り組ませることが大切です。
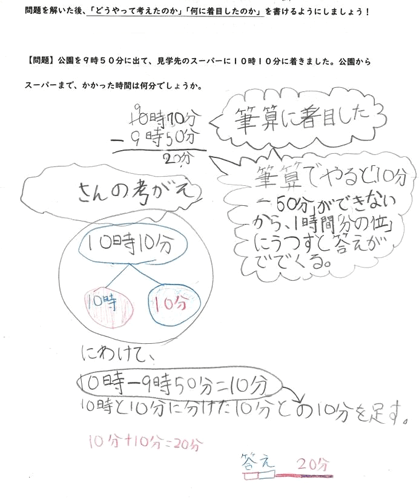
2時間目は、ワークシートを配り、個別学習を行いました。下の写真は、実際に子どもが書いたノートです。
A3用紙の左側には問題が書いてあり、右側には、解いた問題を発展させるスペースをつくりました。
左側に書いてある問題は「公園を9時50分に出て、見学先のスーパーに10時10分に着きました。公園からスーパーまで、かかった時間は何分でしょうか」という問題です。ただし、問題の前に「問題を解いた後、『どうやって考えたのか』『何に着目したのか』を書けるようにしましょう!」と書いておきました。最初からうまく書ける子どもはいませんが、「答えが合っていたらいい」ではなく、自分の思考の過程を表現することを意識させることが大事なのです。そのためには、自分の思考の過程を言語化するための観点を示しておくことです。そこで私は、上の2つの観点を子どもに示したのです。
ノートの右側は、最初に解決した問題を発展させるためのスペースです。しかし、「問題を発展させてみましょう」と子どもに伝えるだけでは、何をしてよいかわかりません。そこで、ここでも問題を発展させるための観点を示しておくのです。私が示したのは「数を変える(例:9時50分→11時20分)」「数の個数を変える(例:9時50分→9時50分30秒)」の2つです。
最初は、目の前の学習内容に直結させ、このぐらい具体的に問題を発展させるための観点を与えた方が、子どもは考えやすくなります。慣れてきたら、「数を変えてみましょう」「数の個数を変えてみましょう」「場面を変えてみましょう」といった、汎用性のある観点を与えていくとよいでしょう。
数学的な見方・考え方を意識させていく
5月に入るころから、少しずつ数学的な見方・考え方を意識させていきます。特に、数学的な見方は大切です。私のクラスでは「着目ポイント」という言葉を使って、数学的な見方を意識させていきました。
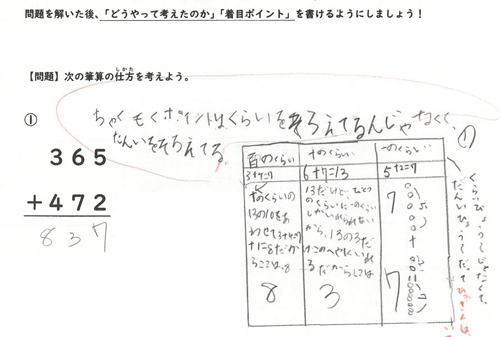
下のノートは5月20日行った個別学習のときに子どもが書いたノートの一部です。
「ちゃくもくポイントはくらいをそろえてるんじゃなくて、たんいをそろえてる」という言葉が書いてあります。これは、既習であるたし算とのつながりが意識されている着目ポイントです。「たし算(ひき算)というのは、同じ単位どうしでなければできない」という原理に気づいている姿です。これは、先述の時計の計算のときの学習が強く影響しています。
着目ポイントというのは、数学的な見方ですから、少し抽象的です。本時の問題であれば、具体的な計算の仕方ではなく、「筆算の意味」や「たし算(ひき算)の原理」といったことです。教師が「どんなところに着目して考えるとよいか」ということを声かけするのは重要ですが、それだけではなかなかできるようにはなりません。やはり、何度も考えたり、いろいろな人の書き方を見たりして学ぶ以外にないのです。自分で着目ポイントを言語化したり、まわりの人が言語化した着目ポイントを読んだり、そして、教師から与えられた観点を参考にしたりしながら、着目ポイントについて考え続けていくことで、少しずつ自分で働かせている数学的な見方・考え方を自覚できるようになり、言語化できるようになるのです。
【参考・引用文献】
・杉山吉茂(2012)『杉山吉茂算数・数学教育論選集 確かな算数・数学教育をもとめて』(東洋館出版社)p.61