- �����I�Ȋw��
- �Z���E���w
�@�u�ʍœK�Ȋw�сv�Ɓu�����I�Ȋw�сv�́A�q�ǂ������ɂ����w�тł���ȏ�A�q�ǂ����w�т�i�߂Ă����Ȃ���Ȃ�܂���B���̂��߂ɂ́A�u�w�ѕ��v���w�ԕK�v������܂��B�ŏ�����u�����Ŋw�K��i�߂܂��傤�v�ƌ����Ă��A�q�ǂ��͉�������悢���킩��Ȃ��ł��傤�B�܂��A�Ԉ�����u�w�ѕ��v���w��ł��܂��Ă͈Ӗ�������܂���B�Ђ�����h�����w�K�����Ă���q�ǂ����A�������̓I�Ɋw�K���Ă����Ƃ��Ă��A����͒m���Ώd�̊w�тɂȂ��Ă��܂��܂��B
�@�u�w�ѕ��v���w�ԂƂ����̂́A�w�K�v��𗧂Ă�Ƃ��A�b�����������w�ԂƂ������Ƃ����ł͂���܂���B���Ȃ��w�K����̂ł���A�ނ���A�e���Ȃ̓����ɉ������u�w�ѕ��v���w�Ԃ��Ƃ��厖�ł��B����ɂ͍���̓����ɉ������u�w�ѕ��v������A�Z���ɂ͎Z���̓����ɉ������u�w�ѕ��v������̂ł��B
���Ȃ̓����ɉ������u�w�ѕ��v�̑��
�@���Ȃ̓����ɉ����āA�e���Ȃŗ{���ׂ��͂Ƃ����͈̂قȂ�܂��B���Ȃɂ���ė{���ׂ��͂��قȂ�Ƃ������Ƃ́A���Ȃɂ���āu�w�ѕ��v���قȂ�Ƃ������Ƃł��B
�@�Z���ŗ{���ׂ��͂́u���K������l�X�ȍl�������g���āA�V�����m����n������́v���ƍl���Ă��܂����A���̗͂�{�����߂́u�w�ѕ��v�Ƃ͂ǂ�Ȃ��̂ł��傤���B
�Z���̋��Ȃ̓����ɉ������u�w�ѕ��v
�@�Z���ŗ{���ׂ��u���K������l�X�ȍl�������g���āA�V�����m����n������́v����Ă邽�߂ɂ́A��Ɉȉ���2�́u�w�ѕ��v��g�ɂ��邱�Ƃ��d�v���ƍl���Ă��܂��B
�@�������w�K
�A�����I�E���W�I�ɍl����
�@�ȉ��A���ꂼ��ɂ��ďq�ׂĂ����܂��B
�@�������w�K
�@�������w�K�Ƃ́A���K�������g���Ȃ�������������A���̉ߒ��ŐV�����m�����q�ǂ����炪�������Ă��w�K�ł��B
�@���́A�Z���̋��ȏ��Ƃ����̂́A�������w�K�̗���ɉ����Ă����Ă��܂��B�Z���̋��ȏ��́A�u�@���i�ۑ�j���A�������̐������B�܂Ƃ߁��C���K���v�Ƃ�������Ɋ�Â��Ď��ʂ��\������Ă��邱�Ƃ������̂ł��B�Z���̊w�K�ɂ����āA�����Ŋw�K��i�߂�ہA���̖������w�K�́u�w�ѕ��v��m���Ă���A�ʊw�K�̂Ƃ����A�܂��̐l�ƈꏏ�Ɋw�K��i�߂�Ƃ����A�q�ǂ����g�Ŋw�K��i�߂邱�Ƃ��ł���悤�ɂȂ�܂��B
�@�������A�ŏ�����A�ʊw�K�Ŗ������w�K�́u�w�ѕ��v�����Ȃ���w�K����q�ǂ��̎p�����҂���͓̂���ł��B��Ď��Ƃɂ����āA���x���������w�K�̗����S���Ōo�����A�u�Z���Ƃ́A��������Ċw��ł����̂��v�Ƃ����u�w�ѕ��v��g�ɂ��āA�͂��߂Ďq�ǂ��͂ł���悤�ɂȂ��̂ł��B
�@��q�̂悤�ɁA�Z���̋��ȏ��Ƃ����̂́A�������w�K�����R�Ƃł���悤�Ȏ��ʍ\���ɂȂ��Ă��܂��B�ł�����A���ȏ��̎��ʂ��g���Ȃ���A�u�Z���Ƃ����̂́A�@���i�ۑ�j���A�������̐������B�܂Ƃ߁��C���K���Ƃ�������Ŋw�K���邱�ƂŁA�V�����m���������Ŕ������邱�Ƃ��ł����v�Ƃ������Ƃ�������̂���ł��B
�@�Z���̋��ȏ��́A�m���邽�߂����̂��̂ł͂Ȃ��A�u�w�ѕ��v���w�ԎQ�l���ł������̂ł��B
�A�����I�E���W�I�ɍl����
�@�������w�K�Ƃ����u�w�ѕ��v���w�Ƃ��Ă��A�����������g�ɂ��Ă��Ӗ�������܂���B�ǂ�ȂɊw�K�̗�������g�ɂ����Ƃ��Ă��A�Z���ŗ{���ׂ��u���K������l�X�ȍl�������g���āA�V�����m����n������́v��{�����Ƃɂ͂Ȃ���Ȃ�����ł��B���̗͂�{�����߂ɂ́A�����I�E���W�I�ɍl����K�v������܂��B
�@�w�K�w���v�̂̉���i�Z���ҁj�ɁA���w�I�ȍl�����́A�u�w�ړI�ɉ����Đ��A���A�}�A�\�A�O���t�������p���A��������ɋؓ��𗧂Ăčl���A�������̉ߒ���U��Ԃ�Ȃǂ��Ċ��K�̒m���y�ыZ�\�����֘A�t���Ȃ���A�����I�E���W�I�ɍl���邱�Ɓx�ł���ƍl������v�i�����Ȋw�ȁA2017�j�Ǝ�����Ă���ʂ�A�����I�E���W�I�ɍl���邱�ƂƂ����̂́A���w�I�ȍl������1�ł��B�����āA���������I�E���W�I�ɍl���邱�Ƃ́A�w�K���e�̌n�����������Z���Ƃ������Ȃ̓������̂����Ȃ̂ł��B
�@���W�Ƃ������t�͕�������Ă��܂����A�z�������Ǝv���܂��B�������A�����Ƃ������t�͂��܂蕷������Ȃ����t�ł͂Ȃ��ł��傤���B
�@�����i1981�j�́A�����Ƃ������t�̈Ӗ��ɂ��āA�ȉ��̂悤�ɏq�ׂĂ��܂��B
�@�u�����v�́A�͂��߂́A������e�Ƃ��āA��̕���ɂ����鐔�w�I�ȓ��e�͂������A�ق��̕���̂��̂ɂ��Ă��A���Ȍ`�łȂ��A�悭��������֘A�Ƃ܂Ƃ܂�̂�����̂Ƃ��Ċw�K�����悤�ɂ������Ƃ�������
�@�v����ɁA�o���o���Ɍ�������̂̒����狤�ʓ_�������o���A�d�v�ȍl�����������o���Ƃ������Ƃł��B����́A�Z���ɂ����āA�ƂĂ��悭�s�������ł��B���ȏ��Ō����u�܂Ƃ߁v�̕������o�����߂ɍs���Ă���̂��A�����I�ɍl����Ƃ����ł��B
�@�܂��A�����i1981�j�́A�����I�E���W�I�Ƃ������t�ɂ��āA�ȉ��̂悤�ɏq�ׂĂ��܂��B
�@�u�����I�v�Ɓu���W�I�v�Ƃ����I�ɂ�݂Ƃ�Ȃ��ŁA�u�����Ƃ������ϓ_�ɂ�锭�W�I�ȍl�@�v�Ƃ����悤�ɂ�݂Ƃ邱�Ƃ��]�܂����B
�@�����I�Ɣ��W�I�Ƃ������t�͕���ł͂Ȃ�����������A�����I���O�Ŕ��W�I����Ȃ̂ł��B�������邱�ƂŔ��W�������̂ł��B����ɂ����ƁA�����甭�W�������Ƃ��Ă��A�������O�ɂȂ���A���W�̉��l�͒Ⴍ�Ȃ��Ă��܂��̂ł��B
�@5�N���ٕ̈��ꕪ���̂����Z�ł���A�l�X�ȉ�@�����ȍl���������A�u�ʕ����āA�P�ʕ����̂������ōl����v�Ƃ������ʂ���l�����������܂��B���̂����ŁA�u�ł́A���̐��l�̕����ł��A���̍l�������g����̂��ȁH�v�ƁA�����������W������Ƃ������Ƃł��B���́u�ł́A���̐��l�̕����ł��A���̍l�������g����̂��ȁH�v�ƍl����Ƃ���ɉ��l������̂ł��B�������̐��l��ς�����A��������������肷�邾���ł́A���܂艿�l�͂Ȃ��̂ł��B
�����I�E���W�I�ɍl����q�ǂ��̎p
�@���ۂ̎q�ǂ��̗l�q�����ƂɁA�q�ǂ��������I�E���W�I�ɍl���Ȃ���w�K��i�߂�l�q���Љ�܂��B�{���H�́A3�N���̈ÎZ�̒P���Ōʊw�K���s�����ۂ̂��̂ł��B
�@�ŏ��ɋ��t����������́A�u44�{29�̈ÎZ�̎d�����l���悤�v�Ƃ������̂ł����B�܂��A���̒��ňÎZ�����ē������o���āA�ǂ�����ē��̒��ňÎZ�������̂������⌾�t�Ńm�[�g�ɏ����悤�ɓ`���܂����B
�@�ŏ��̖������������_�ŏ�����Ă����̂́A���̂悤�ȓ��e�ł����B
�@1�N���̂���Ɋw�K�����A�������ڎZ���v���o���āA����̂������ɕ����邱�ƂɋC�Â��Ă��܂����B�����āA�܂��̐l�Ƙb�������Ă������ŁA�����̎q�ǂ��������u�������ڎZ�����āA����̂������ɕ�����v�Ƃ����l���������ʂ�����Ȑ��w�I�Ȍ����ł��邱�ƂɋC�Â��Ă����܂����B
�@���́u����̂������ɕ�����v�Ƃ������Ƃ��A�ʂ��Ƃɕ����Ă��邱�ƂƓ������Ƃ��ƋC�Â��A�u���炢���ƎZ�v�Ɩ������Ă���q�ǂ������܂����B
�@�܂��A���̂悤�Ȃ��Ƃ��������q�ǂ������܂����B���̎q�ǂ��́A1�N���̌J��オ��̂��邽���Z�̊w�K�Ƃ̋��ʓ_�ɖڂ������Ă��܂��B�����āA�����傫���Ȃ��Ă��A�ʂ��ƂɌv�Z���邱�Ƃ͓����ł��邱�ƂɋC�Â��Ă��܂��B���K�����Ɩڂ̑O�̊w�K�Ƃ̋��ʓ_�������o���Ă���p�ł���A�����I�ɍl���Ă��邱�Ƃ̕\��ł��B
�@�q�ǂ��́A���Ɂu�������ڎZ�����āA����̂������ɕ�����i���炢���ƎZ�j�v�Ƃ������w�I�Ȍ������ǂ�ȂƂ��Ɏg����̂����l���Ă����܂����B���Ă���ƁA���̔��W�̂��������A�q�ǂ��ɂ���ĈقȂ�܂����B�܂����u�w�K�̌����v���s���Ă���p�ł����B
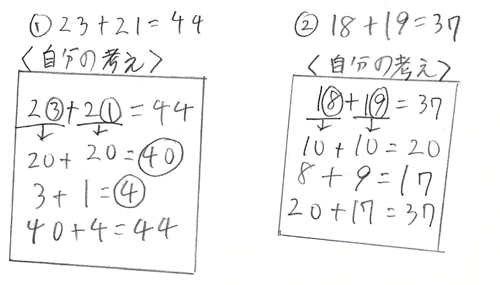
�@���̃m�[�g���������q�ǂ��́A�u����ς��Ă݂悤�v�ƍl���A�u23�{21�v�Ɓu18�{19�v�Ƃ������������Ă��܂����B2���{2���̂܂܂Ȃ̂ł����A����ς��Ė��W�����Ă���̂ł��B���ꂪ�A��ԃV���v���Ȕ��W�̂������ł��傤�B
�@���̂悤�Ȕ��W�̂������������q�ǂ������������܂����B����́A�������R���ɑ��₵�A����ɁA��ʂ܂œ���Ă��܂��B
�@���̂Ƃ����A2���{2���̈ÎZ�Ŏg�����u�������ڎZ�����āA����̂������ɕ�����i���炢���ƎZ�j�v�Ƃ����l�������g���Ă��邱�Ƃ��킩��܂��B�܂��A��ʂ�����ꍇ�̌v�Z�̎d����������Ă���A���R�ƊT�O���L���ɂȂ��Ă��邱�Ƃ��킩��܂��B
�����E�l���������邱�Ƃ��A���Ȃ̓����ɉ������͂�{�����ƂɂȂ���
�@�q�ǂ����������W��������̖������āA�u�Ȃ���Ȃ��̂��v�Ǝv�����������邩������܂���B�m���ɁA���Ƃ��Ă͂���ł��v�����悤�Ȃ��̂ł��B�������A���t������ꂽ���������ďI���̂ł͂Ȃ��A�ŏ��ɉ������u44�{29�v�Ƃ����v�Z�Ŏg�����l���������Č������u�������ڎZ�����āA����̂������ɕ�����i���炢���ƎZ�j�v�Ƃ������w�I�Ȍ������ӎ����āA�q�ǂ����炪���W���������Ƃ̉��l�ɖڂ������Ă��炦����Ǝv���Ă��܂��B
�@�����Ɏ��������́A���ׂĎq�ǂ������甭�W�����đn��o�������̂ł��B�����������A�q�ǂ�������w�K��i�߂�o���̐ςݏd�˂��A�Z���ŗ{�������u���K������l�X�ȍl�������g���āA�V�����m����n������́v�Ɍ��т��ƍl���Ă��܂��B
�y�Q�l�E���p�����z
�E�����Ȋw�ȁi2017�j�w���w�Z�w�K�w���v�̉���@�Z���ҁx�i���{�����o�Łjp.23
�E�������O�i1981�j�w�Z���E���w����Ɛ��w�I�ȍl�����x�i���q���[�jp.40�A126