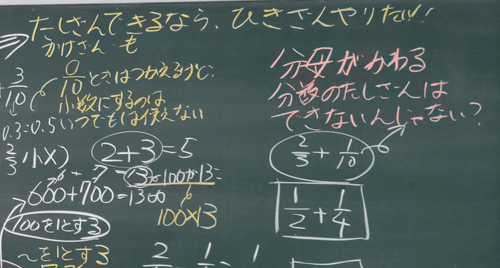数学的活動のAとDの局面の重要さ

　算数科の目標の中に「数学的活動を通して，数学的に考える資質・能力を育成することを目指す」（文部科学省、2017）と示してある通り、算数科の学習は数学的活動を通して行われることになります。ですから、個別学習や自由進度学習を取り入れたとしても、子どもの学習が数学的活動になっている必要があるのです。
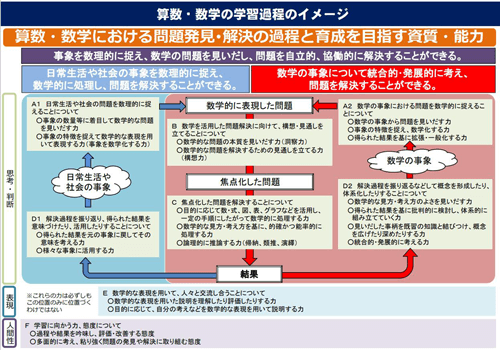
　では、数学的活動とは何か、いま一度確認してみましょう。以下が「ぐるぐるの図」と呼ばれる、数学的活動のサイクルを示した図（文部科学省、2016）です。

　数学的活動は、A〜Dの4つの局面で構成されていますが、重視すべきはAとDの局面です。齊藤（2021）も、数学的な見方・考え方を働かせることによって問題設定から課題解決へ向かうＡの局面と、学びの中で育つ数学的な見方・考え方を意識しながら、より質の高い経験を獲得するＤのプロセスの重要性を述べています。
　Aの局面は、問題を数学化する場面で、「何のためにこの問題を解くのか？」と、子どもが「問題の意識化」をする場面です。Dの局面は、統合・発展をする場面で、子どもが既習事項との共通点を見つけたり、解決した問題を発展させて新たな問題を見いだしたりして「学習の体系化」をする場面です。
　算数の学習を自ら進められるようになるためには、「問題の意識化」と「学習の体系化」が必要なのです。この2つが自分でできるようになれば、解決した問題から問題が生まれ、子どもが自分で学習を進められるようになるのです。

AとDの局面を重視した一斉授業

　算数において、子どもが自分で学習を進められるということは、子どもが数学的活動を回せるようになるということです。個別学習においても、子どもが数学的活動を回せるようになるためには、AとDの局面を意識しなければなりません。しかし、何も指導しなければ、AとDの局面を意識して個別学習をするようにはなりません。そこで、AとDの局面を意識した一斉授業を行い、算数における「学び方」を学ばせていくのです。
　下の板書の写真は、３年生の分数の加法・減法の学習を一斉授業で行った際のものです。

　この学習の前に、単元内において、「分数は、『1／○のいくつ分』と考えることが大事」ということを共有していた際、「『1／○のいくつ分』と考えることはたし算をしていることと似ているから、分数でもたし算ができると思う」という発言がありました。そこで「今まで学習した整数や小数のたし算のように、分数でもたし算はできるのか？」という課題意識を子どもがもちました。本時に入る前に、単元内でAの局面が行われていたということになります。この「分数でもたし算はできるのか？」ということを授業の導入で再確認したうえで、本時の学習に入りました。その際の板書が、以下です。

　本時の問題は「2／10Ｌのジュースと3／10Ｌのジュースを合わせると何Ｌになるでしょうか」というものでした。しかし、Aの局面を行うことで、「2／10＋3／10を何のためにやるのか？」という「問題の意識化」が行われました。単に答えを出すだけでなく、「分数のたし算はできるのか？」という課題をもって問題に取り組むことができるようになったのです。
　Aの局面をしっかりと行い、「問題の意識化」ができるようになった子どもは、他の子どもの解法に対して批判的思考が働くようになります。本実践において、「2／10＋3／10を0.2＋0.3にして、0.5にしました」という解法の説明がありましたが、他の子どもから「それは分数のたし算になっていないから、分数のたし算の説明になっていない」という意見が出されました。この発言は、まさに「何のためにやっているのか？」という「問題の意識化」がなされていることが確認された発言でした。
　「1／10を1とする」という数学的な見方を働かせることにより、2／10＋3／10を既習である2＋3という整数の加法にすることで問題解決がなされた後、子どもは既習事項である小数や整数の加法との共通点に目を向けていきました。それは、統合している場面ですから、Dの局面と言えます。そのときの板書が次の写真です。

　整数・小数・分数すべての加法において使える「〜を1とする」という数学的な見方を「最強のぶき（武器）」という表現で統合していました。
　そして、「たし算ができるなら、ひき算もできそうだからやってみたい！」「それなら、かけ算やわり算でもできると思う！」と、解決した問題を基に、新たな問題へと発展させていました。まさにDの局面です。中には、「分母が違う場合は、『〜を1とする』は使えないのではないか？」と異分母分数のたし算について考えようとする子どもも現われました。問題を発展した際の板書が、次の写真です。

　統合・発展を行うDの局面を行うことによって、新たな問題が子どもの中で生まれ、次の回転のAの局面につながっていくのです。本実践であれば、「〜を1とする」という数学的な見方を働かせることにより、同分母分数の加法・減法ができた子どもは、次時の個別学習において、分数を使った乗法や除法に取り組むことになりました。「〜を1とする」という数学的な見方を働かせて学習を進めていくことによって、「どこまで『〜1とする』という数学的な見方が使えるのか？」「『〜1とする』という数学的な見方が使えない場合はどのようなときか？」といったことを考え、「学習の体系化」を行っていったのです。

AとDの局面を意識させるために行う発問

　本連載において、何度も述べていますが、「個別最適な学び」と「協働的な学び」を実現するためには、一斉授業において「学び方」を学ばせることが必要です。「学び方」は教科の特質によって異なります。算数における「学び方」とは数学的活動のことです。しかし、「ぐるぐるの図」を子どもが理解することは難しいでしょうし、教師にとっても、A〜Dの局面をすべて意識しながら授業をするのは難しいでしょう。
　そこで、まずは「何のためにこの問題を解くのか？（問題の意識化）」というAの局面と、「既習事項と共通する大切な数学的な見方は何か？」「共通する大切な数学的な見方を働かせれば、どんな問題が解けそうか？」と学習を統合・発展（学習の体系化）させていくDの局面を、子どもに意識させるのです。そのために、「何のために問題を解くのか？」「前の学習との共通点は何か？」「前の学習との共通点を使えば、どんな問題が解けるのか？」といったことを発問し、AとDの局面を子どもに意識させていくのです。一斉授業において、その発問を何度も繰り返すことによって、子どもは少しずつ算数の「学び方」を身につけていくのです。

　次回は、次時に行った個別学習の様子について述べていきますので、ご期待ください。