この授業のねらいは、 (分数)×(分数)の計算の仕方を理解させることです。しかし、ここで言う「(分数)×(分数)の計算の仕方を理解させる」とは、という計算方法を単に覚えさせることではなく，計算の仕方をつくり上げていくプロセスを重視しています。そこに「既習事項を活用して、筋道立てて考える」という算数の学習の重要な価値が存在するからです。
　そこでこの授業では、小数のかけ算の際に用いた「整数に直して計算する」というアイデアを引き出し、それを活用することで分数のかけ算の計算の仕方をつくり上げていきます。

1　自然に既習のアイデアと関連付けられる課題提示と発問

　まず、あえて(分数)×(分数)の式だけを提示し、答えを尋ねます。そして、それが未習の計算であることを確認したうえで、分数を小数に変換できることに気付かせ、積を求めていきます。解決する際に用いる「整数に直して計算する」というアイデアが分数のかけ算でも活用できるため、ていねいに進めていきます。

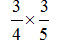Ｔの答えはなんですか？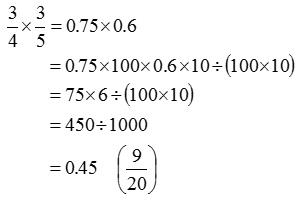

2　既習のアイデアと新たな問題の解決の関連付け

　小数に直すことができる分数で導入したことで、その方法はすでに板書に示されています。そこで、次に分数を小数にできない場合にはどうするかを考えていきます。その中で、先に用いた「整数に直して計算する」というアイデアが活用できないかということに気付かせます。

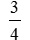Ｔなるほど。じゃあ、はどうすれば整数にできるかな？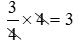

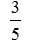Ｃそうか、だったらは5をかければいい。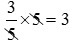

　
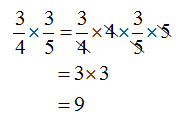
　ここからは、商分数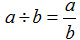を活用することで積を求めるとともに、の計算形式になることを明らかにしていきます。

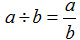Ｔを使って分数の形にするとこうなります。

　以上のように、小数と分数を関連付けることで、解決の見通しをもつことができ、演繹的に分数のかけ算公式を見いだすことができました。
直面した未知の問題に子どもが向き合えるかどうかは、“解決の見通し”がカギになります。この場面に限らず、「似たような問題はなかったか。そのときの解決方法が使えるのではないか」と考えられれば、未知の問題でも解決の見通しをもつことができます。
　このように、算数の授業を組み立てる際には、目の前の問題を解決させるだけでなく、「問題を解決する手段を手に入れさせ、それをいかに使えるようにするか」ということを念頭に置くことが重要です。