- �Ƃ��Ă����Z������
- �Z���E���w
�{���̂˂炢
�@1�ڐ���̑傫���̎����ɂ���āA�܂���O���t�̌��������ς�邱�Ƃ𗝉����邱�Ƃ��ł���B
��
���̂Ƃ��Ă����|�C���g
- 2�̐܂���O���t���r���₷���悤�A���킹�ɂ��Ē���B
- ���i���ʋC���ω��̕\�j�����o���ɂ���B
- �V���s�Ɠߔe�s�̐܂���O���t��1���̃O���t�p���ɋL�����A�Ⴂ���r���₷������B
���Ƃ̗���
12�̃O���t����ߔe�s�̃O���t��I�������i5���j

�@��1���ł́A���Ȃ̃w�`�}�̐����̊w�K�Ɗ֘A�����Ȃ���A���ԂƋC���̕ω���_�O���t�ɕ\���A��������܂���O���t�ւƂȂ����B�܂���O���t�̗ǂ��Ƃ��āA�ω��������₷�����Ƃ𑨂��Ă����B
�@��2���ł́A�܂���O���t�ƕ\�̃f�[�^�Ɣ�ׂȂ���A�܂���O���t�̌X���ɂ����������o���Ă����w�K���s�����B�X����ƋC���̕ω��̎d�����Ȃ����Ă��邱�ƂɋC�t���Ă������B
�@�{���ł͂܂��A�����Ƃ��ĉ��ꌧ�ߔe�s�̃C���[�W���m�F���邱�Ƃ���͂��߂��B
�i�ߔe�s��A�HB�H�Ɣ�������A�j�ߔe�s���Ăǂ�ȃC���[�W�H
��N���g�����C���[�W�B
�V���s�����g�����͂��B
�@2�̃O���t����āc
�ߔe�s�͂ǂ������ȁH
A����Ȃ����ȁB�C�����������B
B���ȁB�C���̕ω�������������B�ł�������ƋC�����Ⴗ����悤�ȁc�B
����݂����ȋC���̃f�[�^�i�\�j���~�����B
�ł́A�ߔe�s�̌��ʋC���ω��̕\�������܂��傤�B

2���ʋC���ω��̃f�[�^�����ƂɃO���t���������i13���j
�f�[�^�����āA���߂Ď����̗�������߂Ă��������B�ߔe�s��A���ȁHB���ȁH
�搶�I�ǂ����ł��Ȃ��Ƃ������������ł����H
�@���ʓI�ɂǂ����ł��Ȃ��Ƃ����ӌ��Ƃǂ������ߔe�s�ł͂Ȃ����Ƃ����ӌ����唼�ƂȂ����B
�iB��I�q���w�����āj�ǂ�����B�ƍl�����̂��ȁH
�ߔe�s�̃f�[�^������ƁA�C���̍ő�ƍŏ��̒l�̍�������������O���t���ɂ₩�ɂȂ�Ǝv�����B
���`�Ȃ�قǁB�m���ɂ���Ȃ�B�Ƃ����̂������邩���B
�ł��A����ς肱�̃O���t�͂���������B������7�E8���̋C���͂ǂ����29���ł���H����Ȃ�O���t�͕���ɂȂ�͂�����B
�����{�����IA��B�����炶��Ȃ��B����͂ǂ������ߔe�s����Ȃ��ˁI
�@���̂悤�ɁA�\�̐��l�ƃO���t�̕ω��̗l�q���ׂȂ���AA��B���ߔe�s�ł͂Ȃ��ƌ��_�t���Ă������B�ԈႢ���w�E������Ⴄ�Ƃ������R��������肷��Ƃ��A�q�ǂ��̓A�N�e�B�u�ɂȂ邱�Ƃ������B
3A��B�̐܂���O���t������ׁA1�ڐ���̑傫���̈Ⴂ�ɋC�t���i12���j
�@�V���s�̌��ʋC���ω��̕\�����ɓ\��AA��B���V���s�̃O���t�ł��邱�Ƃ�������BA�͂����ɔ[�������q�ǂ��������������AB���V���s���Ƃ������Ƃɂ͈�a���������Ă���q�����������B
�iB���V���s���Ƃ������Ƃ��j�����H�ǂ������V���s�̃O���t�Ȃ̂ɂǂ����Ă���ȂɈႤ�́H
�@�V���s�̃f�[�^��B�̃O���t������ׂ鎞�Ԃ��Ƃ�B
�������������IB�̃O���t��1�ڐ���̑傫�����Ⴄ�B
1�ڐ���̑傫���ɒ��ڂ����ˁB�݂�Ȃǂ��������Ƃ������邩�ȁH
�{�����IA��1�ڐ��肪1�������ǁAB��1�ڐ��肪2�����B
�ߔe�s���O���t�ɂ��Ă݂����B�搶�A�O���t�p�������������B
�@����͕ʂ̃O���t�p����z��̂ł͂Ȃ��A���炩���ߔz�z���Ă������V���s�̃O���t�Ɠ����Ƃ���ɓߔe�s�̃O���t���������邱�Ƃɂ����B2�̃O���t�����Ԃ��ƂŁA����Ɂu��ׂ�v�Ƃ������_�����܂��B
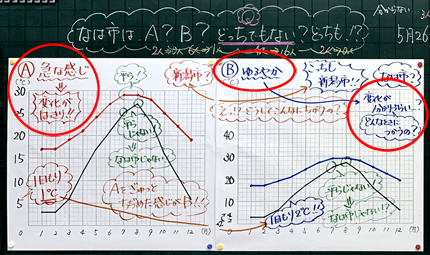
4�ߔe�s�̃f�[�^��܂���O���t�ɕ\���i15���j
�@�ߔe�s�̃f�[�^��܂���O���t�ɕ\������
������ׂĂ݂Ăǂ������܂������H
B�̐܂���O���t��A���M���b�Ək�߂��������ˁB
����ς�A�̕����}�Ȋ����ŁAB�͊ɂ₩�ȃO���t�ɂȂ�ˁB
����̂悤�ȋC���̕ω���\���Ƃ��ɂ�A��B���Ƃǂ����̕\�������������ȁH
�������́u�}�Ȋ����v�ɕt�������ŁA�ω����͂�����ƌ����̂�A��1�ڐ��肪1���̕����Ǝv���B
�ڐ���̑傫����1���ς�邾���ł���ȂɌ��������ς��ˁB
��������A����B�̂悤��1�ڐ���̑傫�����傫���O���t���Ăǂ������Ƃ��Ɏg���́H
�ω���������Â炢�O���t�Ȃ�Ďg��������́H
�������낢�^�₾�ˁB�����1�ڐ���̑傫�����傫���O���t�ɂ��Đ[���l���Ă݂悤���B
�@�Ō�ɏo���^��ɂ��Ă͎����Ɉ������ƂƂ����B���̎��Ԃł́A�����g�̐��܂ꂽ�����猻�݂܂ł�5�N���Ƃ̐g���̕ω����f�[�^�Ƃ��Č������B�����āA�u�݂�Ȃ����̃f�[�^��܂���O���t�ɕ\���Ƃ�����A1�ڐ���̑傫�������p�ɂ���H�v�Ɩ₢�������B1�ڐ���1�p�ɂ���Ɠ������q�����Ȃ����Ƃ��m�F������ŁA�u�ǂ�����1�ڐ���̑傫����1�p�ɂ��Ȃ������́H�v�Ɩ₤���ƂŁA���̂Ƃ����̂Ƃ��̃f�[�^�̑傫�����l���āA�ω��������₷���Ȃ�悤��1�ڐ���̑傫��������Ƃ悢�Ƃ������ƂɋC�t�������B
���Ƃ̂Ƃ��Ă����|�C���g
�@����ӎ������̂́A�������o���ɂ��邱�ƁB�N�������͕�����Ȃ��Ƃ��납��X�^�[�g���邱�ƂŁA�S���̑��ꂪ�����B�����āA�f�[�^�̕K�v�����q�ǂ����������Ƃ��Ɏ��̏������B�f�[�^��ǂݎ��ۂɂ́A�\�̃f�[�^�ƃO���t�̑o��������l���邱�Ƃ�����Ǝq�ǂ������͂��ڂ낰�ɗ������Ă���B
�@�܂��A�V���s�Ɠߔe�s��2�̃f�[�^��ڐ���̑傫����ς��A���ꂼ��1�̃O���t�p���ɕ\�����ƂŁA�ڐ���̑傫���ɂ��܂���O���t�̌������̈Ⴂ���͂�����ƌ����B���̈Ⴂ�Ɏq�ǂ����C�t���Ă�����悤�ȓW�J���ӎ������B