「教科に向かう主体性」を養うための「単元末の『探究的な学習』」とは

　石井（2024）は、学習の動機づけに関わる入り口の情意の1つとして「勉強に向かう主体性」があり、学習の結果生まれ、学習を方向づける出口の情意の1つとして「教科に向かう主体性」があると述べています。計算練習を自ら行う子どもには「勉強に向かう主体性」があるとは言えますが、「教科に向かう主体性」があるとは言えないでしょう。算数科における「教科に向かう主体性がある」状態というのは、第1回で暫定的に定義した「子どもが『数学的な見方・考え方』を働かせながら、習得した知識及び技能を活用することを通して、新たな問いをもつ学習」をしている状態であり、自ら算数科の学びを創り出している姿といってもよいでしょう。
　前回（第2回）では、「日々の『探究的な学習』」の実践を紹介しました。日々の学習において、「探究的な学習」をしていると、１時間ごとに「もっと考えたい！」といった探究しきれないことや、「どうしてこうなるんだろう？」といった疑問が残ることも多くなります。理想的には、次の時間にその続きができればよいのですが、前回述べた通り、次の時間が個別学習であっても、最初の問題は全員同じにしているので、その続きをさせてあげられないこともあります（最初の問題を全員同じにしている理由は、「協働的な学び」をやりやすくして数学的な見方・考え方を多くの子どもが働かせられるようにするため、すべての子どもにやるべき学習内容を保証するため、などです）。もちろん、次の個別学習で、本時の最初の問題を解決した後に、前時に探究したことの続きをやる子どももいますが、時間的に余裕がない子どももたくさんいます。
　そこで、単元内の個別学習で行ってきた「探究的な学習」の中で、「もっと考えたい！」「どうしてこうなるんだろう？」ということを、思う存分取り組む時間を単元末に１時間設けています。

数学的な見方・考え方を働かせた単元末の「探究的な学習」の様子

　今回は、前回ご紹介した６年「文字式」の単元末に行った「探究的な学習」の実践をご紹介します。前回の連載とあわせてご覧いただければと思います。
　前回もお伝えした通り、私は、単元の導入で数時間一斉授業を行い、これから始まる単元において働かせる数学的な見方・考え方を学級全体で共有します。そして、「一斉授業で共有した数学的な見方・考え方が使えるかな？」という意識を子どもにもたせたうえで個別学習を行い、その中で、日々の「探究的な学習」を行っているのです。単元末の「探究的な学習」も、基本的にはこの流れの延長線上にあると考えています。
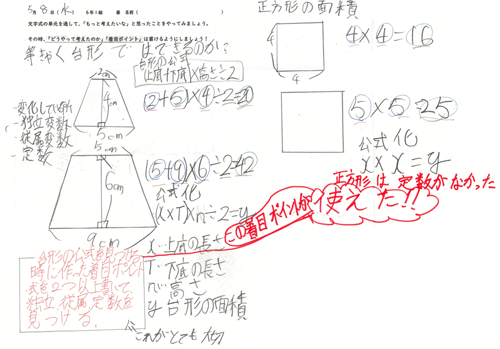
　次の写真１は、前回ご紹介したノートを書いた子どもが、単元末の「探究的な学習」で書いたノートです。

　本実践は、「文字式」の４時間目に行ったものです。前回もご紹介した通り、この子どもは、前時（３時間目）に「円周を求める方法を、xとyを使って式に表しましょう」「１ｍが3kgの鉄の棒の長さと重さの関係を、xとyを使って式に表しましょう」という問題を扱った個別学習をした後の振り返りで、「次は面積を求めてみたい!!」と書いていました。そのことを、単元末の「探究的な学習」で行ったのです。
　ノートの左下には、本単元で働かせてきた独立変数、従属変数といった数学的な見方が書かれるとともに、式を２つ以上書いてそれらを見つけるといった数学的な考え方についても書かれていることがわかります。また、定数がない場合もあることに気づき、数学的な見方を成長させていることがわかります。
　次の写真２のノートを書いた子どもは、1・２時間目で扱った正方形・正三角形に並べた●の個数の求め方を文字式で表す学習の続きをしていました。この子どもは「正方形、正三角形が同じような文字式でできたから、他の形でも同じようにできるのか？」ということを探究していました。その結果、「ひし形は同じようにできるけれど、平行四辺形はできない」ということを発見しました。それだけでなく、平行四辺形に並べた●の個数の求め方を文字式に表したり、図形の性質との関係についても考えたりしていました。

問題を発展し、「探究的な学習」につなげるための3つの視点

　探究をするためには、問題を発展させるための視点を提示するとよいです。主な視点としては、「数を変える」「数の個数を変える」「場面を変える」という３つの視点があります。
　例えば、１人目の子どもは、まず「3時間目に学習したことを、面積でもできるかやってみよう」と考えたので、「場面を変える」ことをしています。次に、「数を変える」という視点で、台形の数値を変えています。
　この3つの視点は、日々の「探究的な学習」においても同様に使うことができますが、問題を発展させるための視点をもてる子どもは多くないので、この3つの視点は私から子どもに伝えています。問題を発展させることに慣れてきたら、「『数をかえる』『数の個数を変える』『場面を変える』ことによって問題を発展させるのは、いつでも使えるか確認するためだよ」と一般化の意識ももたせていきます。

「もっと考えたい！」「どうしてこうなるんだろう？」がない子どもへの支援

　すべての子どもが「もっと考えたい！」「どうしてこうなるんだろう？」と思えるかといえば、そうではありません。慣れないうちは、多くの子どもが問題を解いたら終わってしまいます。そのため、子どもたちには「だれかがやっていることを一緒にやってもいいよ」と声をかけています。そのかわり、「だれかがやっていることをノートに写して終わりではなく、一緒に考えたり、教えてもらったことを自分なりに理解してからノートに書いたりするんだよ」と伝えています。
　また、メモ程度ですが、子どもたちがやっていることを黒板（写真３参照）に書くこともします。この板書は、探究することが思いつかない子どもへのヒントになるのです。

　自分で「探究的な学習」ができない子どももいます。それでも、「これをやりなさい」と言われたことをやるのではなく、少しでも「自分で選択する」という学習習慣を身につけていってほしいのです。