算数科における「探究的な学習」を行ううえでの数学的な見方・考え方の必要性

　前回、算数科における「探究的な学習」の捉えを以下のように捉え直しました。

　算数科における「探究的な学び」を行うためには、子どもが数学的な見方・考え方を働かせることが必要です。そして、なかなか探究が進まない、もしくは、そもそも始めることができない子どもにとっては、数学的な見方を働かせることが、探究のきっかけになります。

数学的な見方・考え方の捉え方

　以下の数学的な見方・考え方は、「小学校学習指導要領（平成29年告示）解説　算数編」（文部科学省、2017a）で述べられている内容です。

　これだけだと、ちょっとわかりにくいと思いますので、具体的な問題を通して説明します。まず、以下の問題を解いてみてください。

　下の□の中に1〜9の数を入れて、縦と横の合計が同じになるように並べましょう。

　解けたでしょうか。この問題は、十字の真ん中の数がポイントになります。並べ方は様々あるとしても、真ん中の数が何になるかで解き方が決まってきます。
　下に解答例を並べましたが、何かお気づきでしょうか。

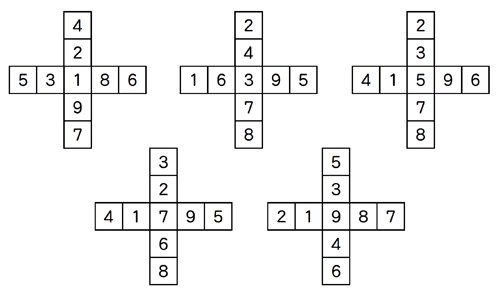
　この問題は、真ん中の数が奇数のときに、縦と横の合計が同じになるように並べることができます。
　では、なぜ真ん中の数が奇数だと並べることができるのでしょうか。1〜9の合計は45です。「縦と横の合計が同じになる」ということは、（45＋真ん中の数）÷2ができるときに並べることができるということです。÷2ができるということは、（45＋真ん中の数）が偶数のときということです。45は奇数だから、真ん中の数が奇数だと、（45＋真ん中の数）は偶数になります。だから、真ん中の数が奇数だと並べることができるのです。
　この問題が解けたら、「真ん中が奇数のときに並べることができるのであれば、偶数のときに並べることができるようにするには、どうすればいいのかな？」と新たな問題を考えることを期待したいものです。
　この問題で働かせている数学的な見方は、奇数・偶数ということになります。奇数に着目して解法を振り返り、様々な解法を統合的に考えることで、「真ん中が奇数なら並べられる」という共通点に気づくことができます。そして、「なぜ奇数なら並べられるのか？」と筋道立てて考えるきっかけにもなっているのです。さらに、「奇数で並べられたのであれば、偶数で並べられるのはどういうときかな？」と発展的に考えることにもつなげることができます。奇数・偶数という数学的な見方を働かせることによって、筋道立てて考えたり、統合的・発展的に考えたりする数学的な考え方が働くのです。

　私なりの数学的な見方・考え方の捉え方を示すと、以下のようになります。

数学的な見方と数学的な考え方の違い

　「数学的な見方・考え方を働かせる」というと、見方・考え方を区別せずに語られることが多いのですが、それぞれ別々に捉えた方がわかりやすいと考えています。
　数学的な見方というのは、学習内容に貼りついているものです。先述の例で働かせた数学的な見方は「奇数・偶数」ですが、学習内容が変われば数学的な見方も当然変わります。
　数学的な考え方というのは、汎用性が高い思考方法です。「なぜそうなるのか？」ということを筋道立てて考えたり、まとめたり（統合）、高めたり（発展）したりするのは、算数科では学習内容を問わず、どの学習でも行う思考方法です。
　「数学的な見方・考え方を働かせる」という話をするとき、汎用性が高いため、数学的な考え方について語られることが多いように感じます。数学的な考え方は、算数科に限らず、他教科においても働かせやすいですし、日常生活にも役立つ思考方法です。具体的な様々な場面から抽象し、物事の共通する重要なことを考える場合、まさに数学的な考え方を働かせていると言えるでしょう。
　しかし、数学的な見方が働かなければ、「なぜ？」と思うこともなければ、統合的に考えて共通点を見つけたり、解決した問題を基に発展的に考えたりすることもできないでしょう。よって、数学的な見方と数学的な考え方の関係は、下図のように捉えるとよいと考えています。

　ついつい、汎用性の高い数学的な考え方にばかり目が向きがちですが、まずは、学習内容に貼りついている数学的な見方を明らかにすることが重要なのです。単元を通して働かせる数学的な見方を言語化することができれば、算数科における「探究的な学習」においても、一人ひとりの子どもが数学的な見方・考え方を働かせられているのかを見取りやすくなります。

算数科の本質とは

　「小学校学習指導要領（平成29年告示）解説　総則編」（文部科学省、2017b）では、各教科等の特質に応じた見方・考え方は「各教科等を学ぶ本質的な意義の中核をなすもの」と述べられています。「教科の本質とはこれである」ということを言いきることは難しいものですが、「各教科等の特質に応じた見方・考え方を働かせること」というのは、教科の本質の捉え方の1つとして、十分に納得できるものだと考えています。数学的な見方・考え方を働かせて学習することは、算数科の本質だと捉えることができると考えています。