算数科における「探究的な学習」をするためには、「子どもに学びを委ねる」必要があります。しかし、いきなり「自分で問題をつくりなさい」「自分で問いをもちなさい」と言われても、子どもは何をしてよいのかわかりません。なぜなら、算数科の特質に応じた「学び方」を身に付けていなからです。
算数科における「探究的な学習」をするためには、算数科の特質に応じた「学び方」を身に付けておく必要があります。そのためには、一斉授業において、算数科の特質に応じた「学び方」を何度も経験し、身に付けることが必要なのです。
「学び方」を学ぶための一斉授業の重要性
1人でも多くの子どもが数学的な見方・考え方を働かせるためには、一斉授業で、数学的な見方・考え方を働かせて学ぶ経験をしっかりと積み重ねることが重要です。
一斉授業には「全員が同じことを共有できる」という長所があります。ということは、一斉授業は、「こういうふうに学ぶといいよ」という「学び方」を全員で共有する場として適しているということです。最初から「自分で学習を進めましょう」と言うだけでは、多くの子どもは「問題を解いて終わり」になってしまいます。それでは、各教科等の特質に応じた見方・考え方を働かせて学ぶ「探究的な学習」はできないでしょう。
算数科においては、数学的な見方・考え方を働かせて、「この学習では、こういうところに着眼するといいんだな(数学的な見方の自覚)」「問題が解けたら、『どうしてそうなるのか?』を考えたり、いろいろな解き方から共通点を見つけたり、見つけた共通点を使って、問題を発展させたりするといいんだな(数学的な考え方の自覚)」といった数学的活動を一斉授業で何度も行うのです。そうしないと、「探究的な学習」が単なるドリル学習・プリント学習に陥ってしまいます。最悪の場合「知識の詰め込み」の学習になってしまう恐れさえあります。
「学び方」を学ぶための一斉授業の一例
6年生の柱体の体積の導入2時間を一斉授業で行いました。写真1は第1時の板書の一部です。
写真1 高さと体積の比例関係を考えた際の板書の一部
四角柱の体積を求める公式である「底面積×高さ=体積」を導いて終わりではなく、「高さと体積の比例関係」という数学的な見方に着目させました。その結果、高さと体積が比例関係になっていれば、四角柱以外にも「『底面積×高さ=体積』という公式が使えるのではないか?」と発展的に考察することができました。
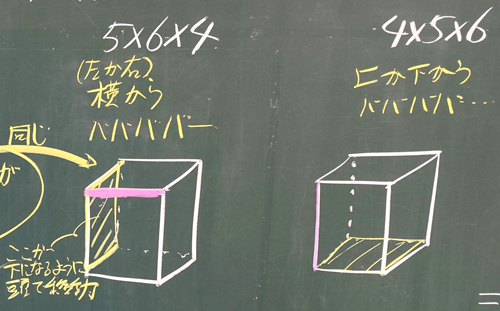
第2時も一斉授業を行い、三角柱の体積も「底面積×高さ=体積」の公式で求められるのかを考えました。写真2は、第2時の板書の一部です。
写真2 柱体の体積の学習の第2時で一斉授業を行った際の板書の一部
第2時では、「底面積×高さ=体積」の公式で求めた三角柱の体積と、前時で学習した四角柱の体積の求め方(四角柱を三角柱2つと考えて、四角柱の体積を求めた後に÷2する求め方)を使って求めた三角柱の体積が同じになることを確かめることで、三角柱でも「底面積×高さ=体積」の公式が使えることを確かめました。
最初、多くの子どもは三角柱の体積を「底面積×高さ=体積」の公式に当てはめて求めて終わっていました。しかし、考えるべきは「三角柱でも、『底面積×高さ=体積』という公式が使えるのか?」ということです。「底面積×高さ=体積」で三角柱の体積を求めるだけでは証明になっていません。
前時に四角柱の体積の求め方は証明されている(5年生で学習した直方体の体積の求め方を根拠に答えを保証)ので、三角柱の体積を保証するためには、四角柱の体積の求め方を根拠にしなければなりません。でも、こういった「学び方」は、子どもだけで気付くことは難しいです。そこで、教師が出て、「算数というのは、今まで証明されてきたものを根拠に、新しいものを証明することが必要なんだよ」と、算数科という教科の特質に応じた「学び方」を明示的に指導しました(写真3参照)。
写真3 算数科の特質に応じた「学び方」を明示的に指導した際の板書
これは、数学的な考え方の1つである「根拠を基に筋道立てて考える」ということそのものです。
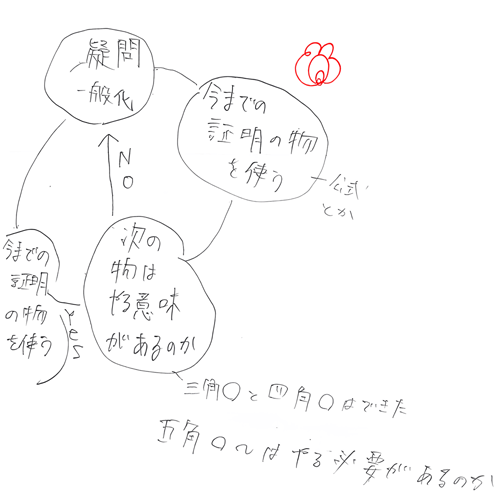
この授業の振り返りには、写真4のような、「学び方」のサイクルを自分なりにまとめた図をかいた子どももいました。
写真4 第2時の振り返りで子どもが書いた「学び方」のサイクルの図
こういった算数科の特質に応じた「学び方」を一斉授業で何度も経験することが、算数科における「探究的な学習」において、数学的な見方・考え方を子どもが働かせられることにつながっていくのです。
根拠を基に筋道立てて考えることだけでなく、統合的・発展的に考察するような「学び方」も一斉授業で何度も経験させることが重要です。いくつかの解法や過去の学習との共通点を考える(統合的に考察する)ことができたら、必ず「この共通する考え方を使ったら、次はどんなことができそうかな?」と発展的に考察することを行うことなどです。こういった一斉授業の積み重ねが、算数科における「探究的な学習」の基盤となります。
「探究的な学習」における「教師が出る場面」とは
1人でも多くの子どもが数学的な見方・考え方を働かせて「探究的な学習」が行えるようにするためには、子どもが「探究的な学習」をしている最中にも、「こういうところを視点に考えてみるといいよ」といった数学的な見方・考え方を意識できるような声かけを細かく行っていく必要があります。そうすることで、「解いて終わり」の学習にならないようにするのです。
子どもが自分で学ぶときにも、数学的な見方・考え方を働かせられようにするためには、教師は子どもにどのような関わりをすればよいでしょうか。なんでもかんでも教師が出てしまっては「探究的な学習」にはなりません。算数科における「探究的な学習」において「教師が出る場面」というのは、「子どもに数学的な見方・考え方を意識させる場面」ではないでしょうか。
一斉授業というのは、単元において最も重要な「教師が出る場面」です。特に単元の最初の数時間で行う一斉授業は重要です。一斉授業の「全員が同じことを共有できる」という長所を生かして、単元を通して働かせる数学的な見方・考え方を全員で共有し、子どもが「こういう着眼点で学習すればいいんだな」と数学的な見方・考え方を意識するためには、教材研究に裏付けされた「教師の出る場面」が重要になるのです。