- �Z���Ȃ̒T���I�Ȋw�K
- �Z���E���w
- �R�����g(0)
�@����́A�A�ڍŏI��ł��B�ߋ�9��ɂ킽���āA�Z���Ȃɂ�����u�T���I�Ȋw�K�v�̗��_����H���܂Ƃ߂Ă��܂����B�����ŏd�v�ɂȂ�̂��u���w�I�Ȍ����E�l�����v���Ƃ������Ƃ����x���q�ׂĂ��܂����B���݁A�����R�̋���ے������ʕ�������オ��A�u���j�I�ȊT�O�v�ɂ��Ċ����ɋc�_����Ă��܂��B�Z���Ȃɂ�����u�T���I�Ȋw�K�v�ɂ����ẮA���́u���j�I�ȊT�O�v�ɂ��čl���邱�Ƃ��s�����ƍl�����܂��B�����ōŏI��ł́A�c�_���́u���j�I�ȊT�O�v�܂��āA�Z���Ȃɂ����đ�Ȃ��Ƃ��܂Ƃ߂܂��B
�@�������A�u���j�I�ȊT�O�v�ɂ��ẮA�c�_���̂��߁A���̒�`�𖾂炩�ɂ��邱�Ƃ͂ł��Ȃ����Ƃ��A���炩���߂��������������B
�Z���Ȃɂ�����u���j�I�ȊT�O�v�̑����ƎZ���Ȃő�ɂ���������
�@�ߘa6�N12��25���ɏo���ꂽ�u������������ɂ����鋳��ے��̊���݂̍���ɂ��āi����j�v�i�������b����j�ɂ́A��ȐR�c�����Ƃ��āA�ȉ��̐}1��4��������܂����B�i�����Ȋw�ȁA2025a�j
�}�P�@����Ŏ����ꂽ��ȐR�c�����i�����Ȋw�ȁA2025a�j
�@��ȐR�c�����̒��́u�@���̍����A�[���w�т��������A������₷���g���₷���w�K�w���v�݂̂̍���v�ɂ́A���X�̎��Ƃɒ���������e������������Ă��܂��B����1�ڂ́��̍Ō�Ɂu�e���ȓ��̒��j�I�ȊT�O���𒆐S�ɁA�ڕW�E���e����w�\�����v�Ƃ�������������܂��B
�@�u���j�I�ȊT�O�v�ɂ��ẮA�u�j�ƂȂ�R���s�e���V�[��T�O�����w���w���j�I�ȊT�O�x�v�i�����Ȋw�ȁA2025b�j�Əq�ׂ��Ă���A�{�A�ڂŎg�p���Ă����u���w�I�Ȍ����E�l�����v�̑������ɋ߂����̂��ƍl���Ă��܂��B�ސ{�i2025�j���A�u���j�I�ȊT�O�v�ɂ��āA�u����͂܂������V�������̂Ȃǂł͂Ȃ��A���łɁw�����E�l�����x�Ƃ����A�C�f�B�A�ŏo���Ă���A���j�I�ȊT�O�ɂ��\�����ɓ�������̂́A�Ⴆ�A���Ȃ́w���q�x��w�G�l���M�[�x�Ƃ��Ď����Ă������̂Ȃ̂ł��v�Əq�ׂĂ��܂��B
�@�������A�����_�Łu���j�I�ȊT�O�v�Ƃ������t�̒�`����܂��Ă���킯�ł͂Ȃ��ł����A�e���ȓ��̓����ɉ����������E�l�����i�ȉ��A�u�����E�l�����v�j�����������l�X�Ȍ������������ƁA�u���j�I�ȊT�O�v���u�����E�l�����v�ƌ������邱�Ƃ͓����������܂���B�����́A����̋c�_�Ɉς˂A�����ł��l�����������Ǝv���܂��B
�@1�����邱�Ƃ́A�q�ǂ����g�ŐV�����m����Z�\������ߒ��ŁA���ʂ���u���j�I�ȊT�O�v��u�����E�l�����v�ɋC�Â��A����ɐV�����������A�������Ă����ߒ����ɂ��Ă������Ƃ́A���ꂩ����d�v�ł����Ƃ������Ƃł��B�Ⴆ�A�{�A�ڂ̍ŏ��ŁA�Z���Ȃɂ�����u�T���I�Ȋw�K�v���u�q�ǂ����w���w�I�Ȍ����E�l�����x�����Ȃ���A�K�������m���y�ыZ�\�����p���邱�Ƃ�ʂ��āA�V���Ȗ₢�����w�K�v�ƁA�b��I�ɑ����܂����B���́u���w�I�Ȍ����E�l�����v���u�Z���Ȃɂ����钆�j�I�ȊT�O�v�Ƃ������t�ɒu���������邱�Ƃ͂���ɂ���A�����_�ł́A���̑�������ύX����K�v�͂Ȃ��ƍl���Ă��܂��B
�u���j�I�ȊT�O�v�́A�q�ǂ��ƈꏏ�Ɍ����Ă�������
�@�u���w�I�Ȍ����E�l�����v�ɂ��Ă��A���낢��ȑ�����������܂��B�w�K�w���v�̂ł͒�`����Ă�����̂́A���̒�`���ǂ̂悤�ɉ��߂���̂��́A�ǂݎ�ɂ���ĈقȂ�܂��B�����ƁA�u���j�I�ȊT�O�v�̑��������A���ꂩ��l�X�ȉ��߂��s���Ă������Ƃ��\�z����܂��B
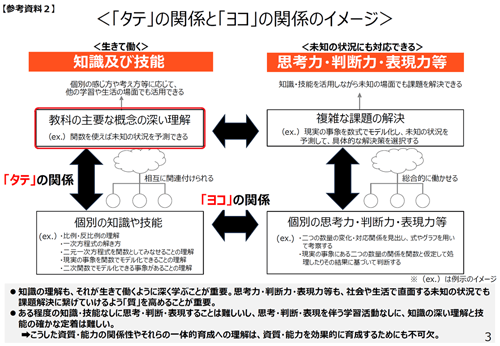
�@�}2�i�����Ȋw�ȁA2025c�j�̐Ԏl�p�g�i�M�҉��M�j�������u���j�I�ȊT�O�v�ƌ�������̂ł��B���̎����́A���w�Z�̐��w�Ȃ��ɍ쐬����Ă��܂��B�ł�����A���w�Z�̐��w�Ȃ̐搶���ɂ̓C���[�W�����₷����������܂���B�������A���Z��⑼���Ȃ̐搶���ɂƂ��ẮA�C���[�W���ɂ�����������܂���B
�}2�@�e���ȓ��̎�v�ȊT�O�̐[�������Ƃ̊W�i�u�^�e�v�̊W�j�ƁA�u�m���y�ыZ�\�v�Ɓu�v�l�́A���f�́A�\���͓��v�̑��݂̊W�i�u���R�v�̊W�j��\�����}
�@���ǁA�u���j�I�ȊT�O�v�Ƃ����̂́A�l�X�ȋ�̗Ⴊ�����āA�͂��߂Ė��炩�ɂȂ���̂ł��B����́A�u�����E�l�����v�������ł��傤�B�ł�����A�u�����E�l�����v��u���j�I�ȊT�O�v�Ƃ����̂́A�q�ǂ��ƈꏏ�Ɍ����Ă��������Ȃ̂ł��B�����w�K�w���v�̂ɂ����āA�e���ȓ��Łu���j�I�ȊT�O�v���������ꂽ�Ƃ��Ă��A������q�ǂ��ɍŏ�����`���Ă��A���܂�Ӗ��͂Ȃ��ł��傤�B
�@�Ⴆ�A�����Z�E�Ђ��Z�ł���A�u�����P�ʂǂ����Ȃ炽���Z�E�Ђ��Z���ł���v�Ƃ����u���j�I�ȊT�O�v�i������u���j�I�ȊT�O�v�ƌ����Ă悢���͂킩��܂��j���q�ǂ��ɍŏ�������Ă��A���̂��߂ɋ�������̂��킩��܂���B�������A�P�����܂����A�w�N���܂����ŁA�����Z�E�Ђ��Z�̊w�K��U��Ԃ邱�ƂŁu�����������Ă��A�����╪���ɂȂ��Ă��A���ǂ́w�����P�ʂǂ����Ȃ炽���Z�E�Ђ��Z���ł���x�Ƃ����͓̂������v�Ƃ������ƂɋC�Â��A5�N���Łu1/2�{1/3�́A�Ȃ����̂܂܂ł͂����Z���ł��Ȃ��̂��낤���H�v�Ƃ����^��������Ƃ��ł��܂����A�u�ǂ�����ĒP�ʁi�����j�����낦��悢�̂��H�v�Ƃ�����@���l���邽�߂̒���_�������Ƃ��ł��܂��B�w�K����Ӗ���A�������̂��߂̒���_�����Ă��Ƃ������Ƃł��B�����āA�u��������A�ٕ��ꕪ���̂Ђ��Z�ł������悤�ɂł��邩�ȁH�v�ƁA���W�����邽�߂̎��_�ɂ��Ȃ�܂��B
�@�ŋ߁A�u�P���̓����ŁA�w�����E�l�����x���Z�b�g����v�Ƃ������t���悭�����܂��B�P���̓����ŁA���̒P���œ�������u�����E�l�����v�����L���邱�Ƃ͏d�v���ƍl���܂����A���t�������I�Ɂu���������w�����E�l�����x�����Ȃ����v�ƌ����Ă��A�q�ǂ��́u���̂��߂ɁH�v�Ǝv�������ł��傤�B
�q�ǂ����u���j�I�ȊT�O�v���g����悤�ɂ��邽�߂ɋ��t�ɋ��߂��邱��
�@�u�w���j�I�ȊT�O�x�Ƃ͉����H�v�Ƃ����c�_�́A���ꂩ�犈���ɍs���Ă����Ǝv���܂��B�u���j�I�ȊT�O�v�̒�`����܂����Ƃ��Ă��A�e���ȓ��̊w�K���e�ɗ��Ƃ����ۂɂ́A���������߂��قȂ邱�Ƃ��\�z����܂��B
�@�܂��A�ǂ̃��x���Łu���j�I�ȊT�O�v�𒊏ۉ����Ă������ɂ���Ă��A���������قȂ邱�Ƃł��傤�B���ۓx�����߂��Ă��q�ǂ��͗����ł��Ȃ��ł����A���ۓx����߂��Ă��A���낢��Ȓm�����Ȃ��č\�������邱�Ƃ��ł��Ȃ��Ȃ�܂��B
�@�������A�q�ǂ����ӎ����A�g������̂łȂ���A�u���j�I�ȊT�O�v���G�ɂ������݂ɂȂ��Ă��܂��܂��B�����Ȃ�Ȃ����߂ɕK�v�Ȃ��Ƃ́A��l�ЂƂ�̋��t�̋��ތ����ł��B1�P�ʎ��Ԃ̋��ތ����ł͂Ȃ��A���Ȃ��Ƃ��P���S�̂����ʂ������ތ����ł��B�ł���A�w�N���܂������n�������ӎ��������ތ������ł�����悢�ł��傤�B
�@2�N���ŁA�����Z�E�Ђ��Z�̕M�Z���w�K���܂����A�u�ʂ����낦�܂��傤�v�Ƃ����w�������邱�Ƃ������Ǝv���܂��B�������A�ʂ����낦��̂͌`���ł��B�Ȃ��A�ʂ����낦�Ȃ��Ă͂����Ȃ��̂ł��傤���B����́A�ʂ����낦��ƁA�P�ʂ����낤����ł��B�\�̈ʂ�10��P�ʂɂ��ĕ\�L����܂��B��̈ʂ�1��P�ʂɂ��ĕ\�L����܂��B������A�ʂ����낦��ƁA�����Z�E�Ђ��Z���ł���̂ł��B�����������Ƃ����t���m���Ă���ƁA�u�����P�ʂǂ����Ȃ炽���Z�E�Ђ��Z���ł���v�Ƃ����u���j�I�ȊT�O�v�������Z�E�Ђ��Z�̕M�Z�ł��g���Ă��邱�Ƃ��A�q�ǂ��ɋC�Â����邱�Ƃ��ł��܂��B
�@�Z���Ȃɂ�����u�T���I�Ȋw�K�v�́A���X�̊w�K�ɂ����čs����ׂ��ł��B���X�̎Z���Ȃ̊w�K�Łu�T���I�Ȋw�K�v���s���邽�߂ɂ́A�q�ǂ����O�̊w�K�Ƃ̋��ʓ_���l���ē����I�ȍl�@�����A���ʓ_����ɐV�������������Ĕ��W�I�ȍl�@�����邱�Ƃ���ł��B�����I�E���W�I�ȍl�@�����邽�߂ɂ́A���̂��߂̒���_���K�v�ł��B���ꂪ�u���w�I�Ȍ����E�l�����v�ł���A�u���j�I�ȊT�O�v�ƌĂ����̂ł��傤�B�Z���Ȃɂ����鋳�t�̎��ƑO�̖����Ƃ��ďd�v�Ȃ̂́A�u���w�I�Ȍ����E�l�����v��u���j�I�ȊT�O�v�𖾂炩�ɂ��A�����̒��ɂ����Ă��������Ȃ̂ł��B
�y�Q�l���p�����z
�E�����Ȋw�ȁi2025a�j��������R�c�� ������������ɂ����鋳��ے��̊���݂̍���ɂ��āi����j�T�vp.2
https://www.mext.go.jp/content/20241226-mxt_kyoiku01-000039494_02.pdf
�E�����Ȋw�ȁi2025b�j��������R�c�� �����������番�ȉ� ����ے����� ����ے������ʕ���i��2��j�z�t�����y�Q�l����1-1�z�Ap.6
https://www.mext.go.jp/content/20250217-mext_kyoiku01-000040050_06.pdf
�E�ސ{���T�i2025�j�u�����R���|�[�g�ƊW�҃C���^�r���[�ŒԂ�@�����w�K�w���v�́w�����ւ̓��x#04�v�i�w�݂�Ȃ̋���Z�p�x���w�فj
https://kyoiku.sho.jp/366151
�E�����Ȋw�ȁi2025c�j��������R�c�� �����������番�ȉ� ����ے����� ����ے������ʕ���i��3��j�z�t�����y����1-1�z�Ap.3
https://www.mext.go.jp/content/20250228-mext_kyoiku01-000040050_02.pdf