学習目標達成のための非認知能力の重要性

　非認知能力を提唱したと言われているジェームズ・Ｊ・ヘックマン（2015）は「人生で成功するかどうかは、認知的スキルだけでは決まらない。非認知的な要素、すなわち肉体的・精神的健康や、根気強さ、注意深さ、意欲、自信といった社会的・情動的性質もまた欠かせない」と述べています。これは、とても納得しやすい話ではないでしょうか。
　このことは、算数の授業においても同じことが言えます。先行知識をもっていなくても、授業で粘り強く考え、まわりの子どもと一緒に考える子どもは、自分で新しい知識・技能や数学的な見方・考え方を発見することができます。

非認知能力とは何か

　OECD（2015）が発表した「Fostering Social and Emotional Skills Through Families, Schools and Communities」をベネッセ教育総合研究所が訳したワーキングペーパー（「家庭、学校、地域社会における社会情動的スキルの育成　国際的エビデンスのまとめと日本の教育実践・研究に対する示唆」）では、「社会情動的スキルは、『(a)一貫した思考・感情・行動のパターンに発現し、(b)学校教育またはインフォーマルな学習によって発達させることができ、(c) 個人の一生を通じて社会・経済的成果に重要な影響を与えるような個人の能力』と定義することができる。これらのスキルは、目標を達成する力（例：忍耐力、意欲、自己制御、自己効力感）、他者と協働する力（例：社会的スキル、協調性、信頼、共感）、そして情動を制御する力（例：自尊心、自信、内在化・外在化問題行動のリスクの低さ）を含んでいる」と示されています。この定義を読むと、冒頭で見たヘックマンの非認知能力と「社会情動的スキル」はかなり近いものだと考えることができます。
　また、中山（2018）は、非認知能力の捉え方について「その時々の状況・環境やこれまでの経緯、そして自分自身の内面（感情など）に左右される力、言い換えれば文脈依存的な力（複数の要素が関連・影響する中で発揮する力）といえるでしょう。『非認知』には数値化困難という『非認知』と情動的で文脈依存的な『非認知』という二重の意味があるのです」と述べているように、非認知能力には、情動的で文脈依存的な「非認知」の意味も含まれているのです。このことからも、OECDが示した社会情動的スキルの定義は、非認知能力の定義と同様のものと捉えられると考えます。

算数で重視すべき非認知能力

　算数で重視すべき非認知能力は、目の前の学習によっても異なると思いますが、どの学習においても大切なことは、目標を達成する力と他者と協働する力だと考えています。　
　私は、算数の学習において、毎時間振り返りシートを書かせていますが、その中に、以下の項目のチェック欄を設けています。

　上記の項目の中で、1つめの「『自分の考え方が本当にあっているのか？』と考えた」というのが、目標を達成する力について、3つめの「友達と一緒に考えたり、友達の考え方との違いを話したりした」というのが、他者と協働する力についてのチェック欄だと考えています。
　このチェック欄を設けたからといって、すぐに目標を達成する力と他者と協働する力が身につくとは考えていません。しかし、このチェック欄を設けることによって、毎時間、自分の考え方について「これで本当にあっているのかな？」と自己調整したり、「自分の考え方だけでなく、友だちの考え方も理解しよう」とまわりの子どもたちの考え方に共感したりすることに意識を向けさせることはできるのではないでしょうか。

算数の学習で非認知能力を働かせる子どもの姿

　6年生の「比例」の学習で、非認知能力を働かせる子どもの姿を紹介していきます。
　本実践は、比例の定義（決まった数×ｘ＝ｙ）や比例の性質について一斉授業で学習した次の時間に、個別学習を行った際の様子です。
　この学習では、まず私から問題を2つ提示しました。問題の内容は以下の通りです。

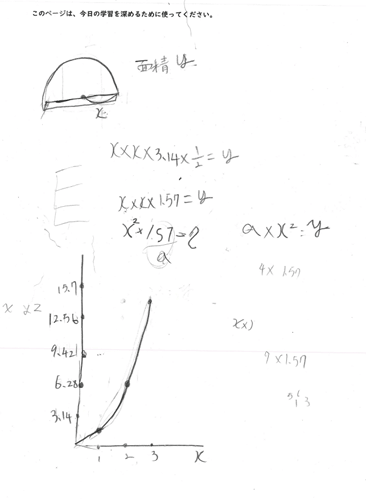
　ある子どもは、最初に私が提示した2つの問題を解いた後、共通する考え方を探り、さらに【問題２】を発展させていきました。具体的には「長方形の横の長さと面積が比例したのだから、円の面積ではどうなるのかな？」と考え、問題を発展させました。つくった問題は「半円の半径をｘcm、半円の面積をｙ㎠として、ｘとｙの関係を式に表す」というものでした。調べてみると、半径と半円の面積が比例関係にならなかったので、他の問題をつくろうとしていました。そこで、私から、「比例関係にならないことはわかったけれど、じゃあ、どんな関係になっていると思う？」と問いかけました。すると、その子どもはグラフを使って、半径と半円の面積の関係を調べ始めたのです。試行錯誤をしたノートの様子が下の写真です。

　このグラフが完成した後、私から「比例のグラフとはどう違った？」と聞くと、「どんどん傾きが急になっていった」と答えた後、「比例はｘが1回だけど、これはｘを2回かけているから急になるんだ」と気づいていました。これこそ、目標を達成する力を発揮した姿と言えるでしょう。半径と半円の面積の関係を粘り強くグラフに表し、意欲的に問題に取り組んだ結果、比例と二次関数（2乗に比例する関数）の違いにまで目を向けることができたのです。まさに、既習事項を使って、新しい知識を創り出した瞬間でもあります。
　実は、このグラフ作成には、まわりの子どもたちの力も大きくかかわっています。最初、どんなグラフになるのかわからなかったこの子どもの様子に、まわりの席の子どもが興味を示しました。そして、この子どもはまわりの子どもたちと一緒にグラフを考えていったのです。他者と協働する力を働かせる姿です。もし、この子どもがまわりの子どもと一緒に考えたり、他者の考え方を受け入れたりすることができなかったら、「半径と半円の面積の関係は比例関係にない」というところで止まってしまい、新しい発見はできなかったはずです。

非認知能力は教科教育を通して育てる

　算数の学習に限らず、やはり非認知能力を備えている子どもは、認知能力も身につけやすいと考えます。先述の比例の実践でもわかる通り、非認知能力が高い子どもは、問題を追究することもできますし、まわりの子どもと協働的に学習することもできるため、目の前の問題について、深く広く考え、理解することができます。そうなれば、自然と知識・技能だけでなく、見方・考え方も豊かになり、認知能力も身についていくのは当然です。
　では、非認知能力を身につけるためには、どうすればよいのでしょうか。行事や総合的な学習の時間を通して、非認知能力を育てることは大切です。しかし、それだけでは不十分です。第一、行事や総合で身につけた非認知能力を算数で発揮することができるとは限りません。やはり、算数で発揮させたい非認知能力があるのであれば、算数の学習の中で育てることが必要だと考えます。自分の解き方を批判的に見ることで新しい発見をする経験。まわりの子どもと一緒に考えることで、解けない問題が解けた経験。そういった経験を積み重ねることで、少しずつ、算数で必要な非認知能力は身についていくのだと思います。それは、他教科でも同じではないでしょうか。ですから、各教科において必要な非認知能力について考え、それを言語化し、子どもが意識できるようにしていくことが大切なのだと考えます。