
- 個別最適な学び
- 算数・数学
個別最適な学びは、自己調整学習と捉えられることがよくあります。子どもにとっての個別最適な学びである以上、子どもが自分の学習しやすい学習形態を選択し、興味・関心に合わせて学習内容を考えていくことは必要です。しかし、すべてを子どもの判断に委ねてもよいのでしょうか。そんなことをしてしまっては、学べるものも学べなくなることは容易に想像できます。価値あるものを価値づけることなく通り過ぎ、知識・技能をひたすら詰め込むことに意識が向かってしまいます。
今回は、個別最適な学びを考える際に、自己調整学習をどのように捉え、どこまでを子どもの自己調整に委ねるのかを考えていきたいと思います。そして、算数において自己調整学習をする子どもの姿を示していきます。
自己調整学習する子どもの姿とは
Zimmerman & Schunk(2014)は「自己調整学習は、学習者たちが自分たちの目標を達成するために、体系的に方向づけられた認知、感情、行動を自分で始め続ける諸過程のことである。学習者たちは自らの目標を設定して、自己指向的フィードバック・ループをつくり出す。そのループによって、学習者たちは自分の有能さをモニターし自分の働きを調整するのである」と述べています。
自分の目標を定め、その目標達成にはどのような知識・技能、数学的な見方・考え方を使うことが適しているのかを考えて行動し、Try & Errorを繰り返しながら、試行錯誤していく学習というとわかりやすいのではないでしょうか。
算数の学習で言えば、目の前の問題を解決するために、どんな既習事項が必要かを考え、どんな解き方をすれば解決できるのかを予想した後に問題解決を試み、うまくいかなければ、何が間違えていたのかを考えながら、また他の解き方を考えていく。そんな子どもの姿でしょう。
算数において自己調整学習をする子どもの姿とは
算数において自己調整学習をする子どもの姿とはどのようなものでしょうか。学習指導要領の算数の目標(3)が、算数における「主体的に学習に取り組む態度」の観点にかかわる目標ですが、それを以下に示します。
数学的活動の楽しさや数学のよさに気付き、学習を振り返ってよりよく問題解決しようとする態度、算数で学んだことを生活や学習に活用しようとする態度を養う。
算数では、これが自己調整学習をする子どもの姿の1つであると言えると考えます。
言い換えると、まさに数学的活動を子ども自身で行っている姿です。学習指導要領の解説(算数編、p.8)にも掲載されており、“ぐるぐるの図”と呼ばれている、算数・数学の学習過程のサイクルをイメージするとよいでしょう。
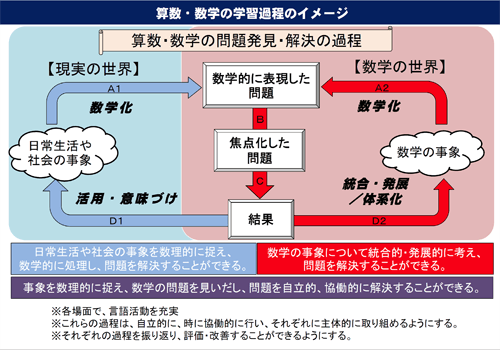
このサイクルを自分で回せるようになれば、算数において自己調整学習ができる状態になっていると言えるでしょう。
個別学習において自己調整学習を行う姿
算数における自己調整学習(数学的活動のサイクルを回す)を子どもが行っている姿を見取るのであれば、やはり個別学習をしているときが最適でしょう。
個別学習における実際の子どもの姿については、第3回と第4回に書いていますので、そちらを参照いただければと思いますが、個別学習の主な流れとして、以下のような展開が考えられます。
①問題を解く
②まわりの人と解き方や考え方を共有する
③大切な、数学的な見方・考え方を見つける
④各自で解いた問題を発展させたり、気になったことを調べたりして、探究する
この①~④の活動を、子どもが教師やまわりの人とかかわりつつ、自分に最適な問題や学習形態を選択しながら進めていけるようにしていくことが、重要であると言えるでしょう。
自己調整学習を支える学習意欲
櫻井(2017)は、自ら学ぶ意欲を2種類の意欲で構成されると述べ、1つを知的好奇心に基づく「内発的な学習意欲」(算数が楽しい、もっと知りたい等)、もう1つを「自己実現のための学習意欲」(自分の将来のために必要、人間として成長したい等)としています。
どちらの意欲をもって学習をするにしても、自ら学ぶ意欲をもつことが、自己調整学習においては必要です。特に、小学校においては、内発的な学習意欲をもたせることが効果的だと考えています(逆に、小学生が、目の前の算数の問題を、自己実現のために解くことはなかなか難しいでしょう)。
算数で内発的な学習意欲をもたせるためには
では、算数において内発的な学習意欲をもたせるためには、どうすればよいでしょうか。これが一筋縄ではいかないことは、教師であればだれもがわかることでしょう。
意識すべきは、以下の2点だと考えます。
①既習事項を使って自分で新しい知識をつくり出せたという経験をすること
②まわりの人と一緒に学習することで、自分1人では気づけなかったことに気づけた経験をすること
①既習事項を使って自分で新しい知識をつくり出せたという経験をすること
1つめは、これまでにも再三述べてきましたが、算数の学習をする価値であり意味です。「算数は、だれかに習わなくても、自分で新しい知識をつくり出すことができる」ということを理解できれば、能動的になります。
下のノートは、6年生で角柱の体積の求め方を学習した際の学習感想の一部です。
この子どもは、体積の学習で働かせた数学的な見方・考え方が、面積の学習で働かせた数学的な見方・考え方とつながっていて、自分ができることを発展させて学習が進んでいることを感じています。この状態になると、自然と内発的な学習意欲が育っていきます。
子どもが既習事項を使って、新しい知識をつくり出していくためには、教師の役割が不可欠です。子どもだけでは気づけないことはたくさんあります。この角柱の体積の学習であれば、子どもは自然と「体積を求められる形にする」という数学的な見方を働かせて体積を求めます。例えば、三角柱で「2つつなげて四角柱にして体積を求めてから、÷2をしました」と説明したとします。ここで終わらせず「どうして四角柱にしたの?」と発想の源を問うのです。そうすると、「体積を求められる形にする」という発想の源に基づいて解いていることを自覚するようになるのです。さらに、その発想の源は、5年生で学習した多角形の面積で、平行四辺形や台形の面積の求め方を考えたときの考え方とも共通していることに気づかせていくのです。
②まわりの人と一緒に学習することで、自分1人では気づけなかったことに気づけた経験をすること
子どもは、1人で学習するよりも、まわりの人と一緒に学習することで、より多くのことを学べることを知っています。実は、その経験が内発的な学習意欲をもたせるためには不可欠だと考えています。
次の学習感想を見てください。
これも、6年生で角柱の体積を学習した際のある子どもの学習感想の一部です。この子どもは、まわりの人とのかかわりを通して、友だちが面積と体積の学習をつなげて考えていたことを知り、「前の学習とむすびつけてかんがえることを意しきする」ことの大切さに気がつきました。教師が言葉で伝えるよりも、子どもはまわりの人の姿を見ることで学ぶことの方が多いものです。
算数で自己調整学習ができると自己効力感ももてる
自己調整学習ができるようになると、子どもは「自分で学習を進められる」と思えるようになります。特に算数においては、「自分で新しい知識をつくり出せる」と思えるようになるので、「自分はいろいろとできる人なのだ!」と思えるようになります。これは「自己効力感」と呼ばれるものです。
ただし、気をつけなければならないことがあります。それは、「自分で学習している姿が見られればそれでよし」としないことです。子どもが様々な学習形態を選択し、既習事項を使って新しい知識をつくり出せるようにするためには、事前の教師の教材研究が不可欠です。なぜなら、ただ問題を解いているだけでは、新しい知識をつくることは難しいからです。子どもが自ら新しい知識をつくり出せるような教材を準備したり、子どものつぶやきを価値づけたりしながら、個別学習をしている子どもの思考を教師は整えるのです。
【参考・引用文献】
・B・J・Zimmerman、D・H・Schunk編、塚野洲一・伊藤崇達監訳(2014)『自己調整学習ハンドブック』(北大路書房)、p.5
・文部科学省(2017)『小学校学習指導要領解説 算数編』(日本文教出版)p.8、22
・国立教育政策研究所教育課程研究センター(2020)『「指導と評価の一体化」のための学習評価に関する参考資料 小学校 算数』(東洋館出版社)pp.9-10
・櫻井茂男(2017)『自律的な学習意欲の心理学―自ら学ぶことは、こんなに素晴らしい』誠信書房、p.3



