
- �ʍœK�Ȋw��
- �Z���E���w
- �R�����g(1)
�@�u�ʍœK�Ȋw�сv�́A�����Ďq�ǂ���1�l�ōs�����̂ł͂���܂���B������������Ƃ���1�l�ōl���邱�Ƃ�����A�킩��Ȃ���܂��̐l�ƈꏏ�ɍl���邱�Ƃ�����̂��A�ʍœK�Ȋw�тȂ̂ł��B
�@1�l�ōl���邱�Ƃ��A�܂��̐l�ƈꏏ�̍l���邱�Ƃ��A�w�K�`�Ԏ��̂��q�ǂ����g���I�����邱�ƂɈӖ�������܂��B���̂��߂ɂ́A���ł��A����Ƃł��w�ׂ�w�K���������̒��ɑ��݂��Ă��邱�Ƃ��K�v�ł��B�܂��ɁA�u�����I�Ȋw�сv���ۏ���Ă���K�v������̂ł��B
�@�ł́A�����I�Ȋw�т��ۏ���Ă�����ƂƂ́A�ǂ�Ȃ��̂ł��傤���B�܂��A���̂��߂ɂ́A�ǂ�Ȃ��Ƃ��ӎ�����K�v������̂ł��傤���B
�ʍœK�Ȋw�т͋����I�Ȋw�т̒��ɂ���
�@�ʍœK�Ȋw�тƋ����I�Ȋw�т̊W�́A�ȉ��̂悤�Ȑ}�Ō���ƃC���[�W���₷���ƍl���Ă��܂��B�����I�Ȋw�т��ł�������O��ƂȂ�A�ʍœK�Ȋw�т���������̂ł��B
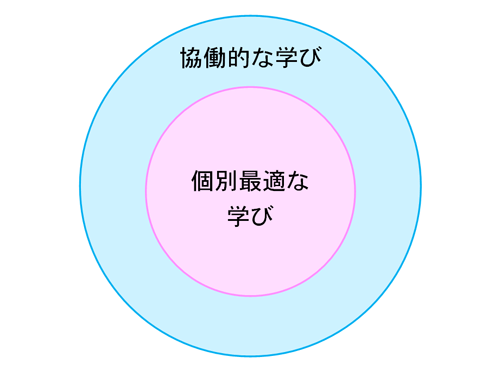
�@2021�N1��26���ɏo���ꂽ�A�u�w�ߘa�̓��{�^�w�Z����x�̍\�z��ڎw���ā`�S�Ă̎q�������̉\���������o���A�ʍœK�Ȋw�тƁA�����I�Ȋw�т̎����`�i���\�j�v�i��������R�c��j�ɂ́A���̂悤�Ɏ�����Ă��܂��B
�e�w�Z�ɂ����ẮA���ȓ��̓����ɉ����A�n��E�w�Z�⎙�����k�̎���܂��Ȃ���A���Ƃ̒��Łu�ʍœK�Ȋw�сv�̐��ʂ��u�����I�Ȋw�сv�ɐ������A�X�ɂ��̐��ʂ� �u�ʍœK�Ȋw�сv�ɊҌ�����Ȃǁu�ʍœK�Ȋw�сv�Ɓu�����I�Ȋw�сv����̓I�ɏ[���� �A�u��̓I�E�Θb�I�Ő[���w�сv�̎����Ɍ��������Ɖ��P�ɂȂ��Ă������Ƃ��K�v�ł���B
�@���̈ꕶ�̒��ɂ���u�w�ʍœK�Ȋw�сx�Ɓw�����I�Ȋw�сx����̓I�ɏ[�����v�Ƃ������t�����d�v���ƍl���܂��B�ʍœK�Ȋw�тƋ����I�Ȋw�т́A�u���ցv�ł͂Ȃ��u��̓I�v�ɏ[������������Ȃ̂ł��B�u����͌ʍœK�Ȋw�сv�u����͋����I�Ȋw�сv�Ɩ��m�ɐ藣������̂ł͂Ȃ��A��̂ƂȂ��Ė����������Ă����p���]�܂��Ƃ������Ƃł��B
�����I�Ȋw�тƂ͉���
�@�����I�Ȋw�тƂ����ƁA�q�ǂ����m���b����������A���ׂ����Ƃ��܂Ƃ߂��肷��p���v�������ԂƎv���܂��B����͂���Ő������̂ł����A�u�����I�Ȋw�т��Ă����������H�v�ƕ������ƁA�����ɍ���̂ł͂Ȃ��ł��傤���B
�@���́A�����I�Ȋw�тƂ́A�����������Ƒ����A���̖����������邽�߂ɁA�_��ɂ܂��̐l�Ƃ������w�����ƍl���Ă��܂��B
�@�����܂��̐l�ƈꏏ�Ɋw�K����̂ł͂Ȃ��A���̑O�ɁA��l�ЂƂ�̎q�ǂ��������������Ƃ��đ����Ȃ���A�����I�Ȋw�тɂ͂Ȃ�Ȃ��ƍl���Ă��܂��B�Ⴆ�A�u���������킩��Ȃ�����ׂ̐l�ɕ����Ă݂悤�v�Ǝv�����Ƃ��A�{���ɉ�������m�肽���Ǝv���Ă���q�ǂ��́A�ׂ̐l�̉�����������A�u�ǂ����Ă����Ȃ�́H�v�Ɩ₢�Ԃ�����A�����ł���蒼���Ă݂��肷��ł��傤�B����A�����������o��悢�Ǝv���Ă���q�ǂ��́A�����āu�������˂��v�ƌ����āA�����������o���ďI����Ă��܂��ł��傤�B�ł�����A�����I�Ȋw�т́A�q�ǂ����g�������������ɂ��邱�Ƃ���n�܂�̂ł��B
�@�����āA�������Ɏ��g��ł���q�ǂ����m���A�������Ƃ������ʂ̖ړI��B�����邽�߂ɁA�_��ɂ�����荇���̂������I�Ȋw�тȂ̂ł��B�܂��͎����̂܂��ɂ���l�Ƙb���Ă݂Ė������Ɏ��g�݂܂��B�������A�܂��̐l���������ł͉����ł��Ȃ���A���̐l�ɂ��b������A�ꏏ�ɍl�����肵�܂��B
�@���̍ۂ̃|�C���g�́A����Ƃł����͂��Ė������������Ƃ������Ƃł��B���̂����l�A�b���₷���l�����łȂ��A�������L���Ă���l�ł���A����Ƃł��������̂ł��B�������邱�Ƃɂ���āA���l�ȍl���ɐG��邱�Ƃ��ł��A���𑽖ʓI�ɉ������邱�ƂɂȂ���܂��B
�@�ȏ�̂��Ƃ܂���ƁA�����I�Ȋw�т̃C���[�W�͉��̂悤�Ȑ}���ƍl���Ă��܂��B

�@�^�ɖ�肪����A��l�ЂƂ�̎q�ǂ������ƌ��������Ă��܂��B�����āA���ʂ̖�����������Ƃ����ړI�Ɍ������āA�q�ǂ������݂����͂������̂ł��B
�@���Ƃɂ����ẮA���̐}�̂悤�Ɏ��g��ł���q�ǂ��̏W�c������������A�W�c���m���e���������Ă��܂��B���������̏W�c�����ł͉����ł��Ȃ�������A���������Ƃ��Ă��������@�Ɏ��M���Ȃ���A���̏W�c�̉������@�Ɣ�ׂ��肵�܂��B�@
�@���ɁA���̏W�c���b���Ă��邱�Ƃ����R�Ǝ��ɓ���A���̏�����ɐV�����l������������A���W�������肷�邱�Ƃ�����܂��B�������Ƃ������ʂ̖ړI����ɂ��āA�q�ǂ����_��ɂ܂��̐l�Ƃ̊W�����ђ����Ă����̂ł��B
�Z���ɂ����鋦���I�Ȋw�т̌��ʓI�Ȏp
�@�����܂ŁA���ۓI�Șb�������Ă��܂������A��������́A���ۂ̎��Ƃɂ�����A�����I�Ȋw�т�����q�ǂ��̎p���Љ�����Ǝv���܂��B
�@�~�̖ʐς̌�������Ď��Ƃł���A�~�̖ʐς̌��������p��������l����ʊw�K���s���܂����B���ƑO���ŁA���ȏ��Ɍf�ڂ���Ă�������R������A���݂��̉������⋤�ʂ����ȍl�������܂��̐l�����Ƌ��L������A���ƌ㔼�ł́A�q�ǂ��͎��ƑO���ʼn��������W�����A���낢��Ȗ��������Ă��܂����B
�@�ŏ��A�����ǂ̐l�Ƃ����������Љ�����A���݂��ɉ����Ă��܂����B���̍ۂ̗l�q�����̎ʐ^�ł��B
�@���̌�A���̔ǂ̎q�ǂ����O���[�v�`���b�g�ɓ��e���������������ƂŁA���̔ǂ̒��̂P�l�́A�l�Ŗ��Ɏ��g�ނ悤�ɂȂ��Ă����܂����B���e���ꂽ�̂́A���̎ʐ^�̖��ł��B
�@1�l�Ŗ��������n�߂��q�ǂ��́A���s���낵�Ă��邤���ɁA�~�Ɖ~���d�Ȃ����Ƃ���̖ʐς����߂��Ȃ����ƂɋC�Â��Ă����܂����B����ƁA�ŏ��ɘb���Ă����܂��̐l�ł͂Ȃ��A�����悤�ɂ��̖��������Ă������̐l�Ƙb���Ȃ���A���O�p�`�̖ʐς̋��ߕ����킩��Ή����邱�ƂɋC�Â��Ă������̂ł��B
�@���O�p�`�̖ʐς����߂邽�߂ɂ́A���O�p�`�̍������킩��Ȃ��Ƌ��߂��Ȃ��̂ŁA�ǂ�����悢�������Ă��܂����B�����Ŏ�����A�O�p���Ƃ������̂����邱�Ƃ����������`���܂����B�������u����͏��w�Z�Ŋw�K���邱�Ƃł͂Ȃ�����A�m��Ȃ��Ă�������v�Ɠ`���������łł��B�������A���̎q�ǂ��́A�����ŃC���^�[�l�b�g���g���āA�O�p���ɂ��Ē��ׁA���O�p�`�̍��������߂Čv�Z���Ă��܂����B
�@���̎q�ǂ��́A�܂��͎����̂܂��̐l�Ƃ������Ȃ���A���ƑO���ʼn��������ɂ��āA�������⋤�ʂ���l���������L���Ă����܂����B�����āA���W������Ƃ���܂ł܂��̐l�ƈꏏ�ɍs���܂����B
�@�O���[�v�`���b�g�ɓ��e���ꂽ���̔ǂ̐l���l�������ɋ������������Ƃ��납��A�l�ł̊w�K�ɐ�ւ��܂����B����ɁA�����Ɠ������������Ă���l�Ƃ������Ȃ���A�����̎����������Ă������̂ł��B
�@���̈�A�̊w�K�̒��S�ɂ́A��ɖ�肪����A�����������悤�Ǝq�ǂ����v�l����p������܂��B�����āA�V�Ԃ��߂�A���Ԙb�����邽�߂ł͂Ȃ��A�������̂��߂ɐl�Ƃ�������Ă��܂��B�������̂��߂ɐl�Ƃ�������Ă���̂ŁA���̏ꂻ�̏�ł������l���_��ɕς���Ă����Ă��邱�Ƃ��킩��܂��B
�@���̂悤�ɁA�����������Ƒ����A���̖����������邽�߂ɁA�_��ɂ܂��̐l�Ƃ������w�т̎p�������o�����߂ɂ��A�u���͌l�ōl���Ȃ����v�u�ł́A������͂܂��̐l�Ƙb�������܂��傤�v�̂悤�ɁA�w�K�`�Ԃ����t���Œ肹���A�q�ǂ����K�v�ȂƂ��ɕK�v�Ȋw�K�`�Ԃ�����悤�ɂ��Ă������Ƃ�����ł��B
�����I�Ȋw�т��������邽�߂̋��t�̖���
�@�����I�Ȋw�т��������邽�߂ɁA���t�̖����͑傫���ƍl���Ă��܂��B�q�ǂ��Ɂu���R�Ɋw�K���Ă�����v�ƌ����Ă��A�Ȃ��Ȃ��܂��̐l�Ƙb����������A���͂��Ė����������悤�Ƃ����肵�Ȃ��̂������ł��B
�@�����ŁA�����I�Ȋw�т��������邽�߂̋��t�̖����Ƃ��đ�Ȃ��Ƃ��A2�q�ׂ����Ǝv���܂��B
�@�l�����̋��ʓ_���l������A���W�������肷��Ƃ����ӎ�����Ă�
�@�g�s�b�N�I�Ȃ������낢���������͓̂���̂ŁA���ȏ��ɍڂ��Ă�����ŏ\���ł��B�������A�������o���ďI���Ƃ����A���������Ƃ��Ɏg�����l�����̋��ʓ_���l����������A���W�������肳����̂ł��i���̔��W�̂������ɂ��ẮA�{�A�ڂ̑�4��Q�Ɓj�B��������ƁA���R�Ƃ��݂��̍l�������m�肽���Ȃ邵�A�ǂ�Ȗ����������̂����C�ɂȂ�̂ŁA�����I�Ȋw�т��N���₷���Ȃ�܂��B
�A�S���I���S�����m�ۂ���
�@�G�C�~�[�E�b�E�G�h�����h�\���i2014�j�́A�S���I���S�����u�֘A�̂���l���⊴��ɂ��Đl�X���C���˂Ȃ������ł��镵�͋C�������v�Əq�ׂĂ��܂��B���ꂪ�����I�Ȋw�т��������邽�߂ɕK�v�Ȃ��̂ł��邱�Ƃ́A���Ƃ��������Ƃ�����l�ł���Αz�������̂ł͂Ȃ����Ǝv���܂��B�q�ǂ������R�ɔ���������A���s�������ꂽ�肷��N���X�ł���A�������Ƃ����ړI�̂��߂ɁA�_��ɂ���Ƃł��C�y�ɂ�����邱�Ƃ��ł���ł��傤�B�N���X�̒��ɐS���I���S�����m�ۂ���̂����t�̖������Ƃ������Ƃł��B
�y�Q�l�E���p�����z
�E��������R�c��i2021�j�u�w�ߘa�̓��{�^�w�Z����x�̍\�z��ڎw���ā`�S�Ă̎q�������̉\���������o���A�ʍœK�Ȋw�тƁA�����I�Ȋw�т̎����`�i���\�j�vpp.18-19
�E�G�C�~�[�EC�E�G�h�����h�\�����A��Òq�q��i2014�j�w�`�[�����@�\����Ƃ͂ǂ��������Ƃ��x�i�p���o�Łj�Ap.12�A153�A157-158
-
- 1
- �Z���J�t�F(�a��N�F)
- 2021/11/26 14:58:57
�����I�w�тƌʍœK���͈�̂Ƃ����w�E�ɂ͓������܂����A�ʂ̈Ⴂ���ǂ����z���邩�Ƃ������Ƃ��d�v���Ǝv���܂��ˁB���̂Ȃ��݂ƌ`�����d�v���ƍl���Ă��܂��B���Ő搶�͌ʂ̈Ⴂ�����z���邽�߂̃L�[���[�h�͉����ƍl���Ă���������̂ł��傤���H���̂��Ƃ�m�肽���Ǝv���܂����B


