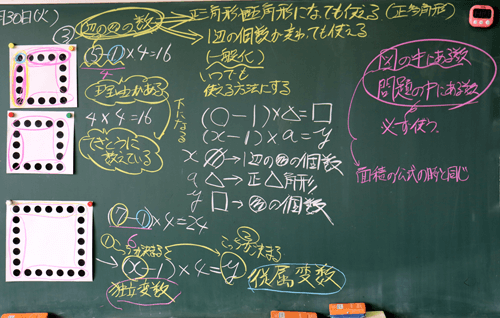- �Z���Ȃ̒T���I�Ȋw�K
- �Z���E���w
- �R�����g(0)
�@�܂Ƃ܂������Ԃ�����āu�w�T���I�Ȋw�K�x�����܂��傤�I�v�Ǝq�ǂ��Ɍ����Ă��A�������Ă������킩��Ȃ��ł��傤�B���ȋ���ɂ����āu�T���I�Ȋw�K�v�����悤�Ǝv���̂ł���A�u���ȂɌ�������̐��v���d�v�ł��B�������A�u���ȂɌ�������̐��v�́A���R�ɂ͈炿�܂���B���t���Ӑ}�I�Ɉ�Ă�̂ł��B���̂��߂ɏd�v�ɂȂ�̂��A�e���ȓ��̓����ɉ����������E�l�����ł��B�e���ȓ��̓����ɉ����������E�l�������q�ǂ����������Ă������Ƃɂ���āA���̋��ȂȂ�ł͂́u�w�ѕ��v���w���A����w�K��n���悤�ɂ��Ă����̂ł��B���̌��ʁA�u���ȂɌ�������̐��v����܂�Ă����̂ł��B
�u���ȂɌ�������̐��v�Ƃ�
�@�q�ǂ����u�����Ƌ��Ȍv�Z�������Ȃ肽���I�v�Ǝv���Čv�Z���K�Ɏ��g��ł���p�́A�Z���Ȃɂ�����u�T���I�Ȋw�K�v�ƌ�����ł��傤���H�@���Ȃ��Ƃ��������悤�Ɠw�͂��邱�Ƃ́A�ƂĂ����炵�����Ƃł��B�������A���w�I�Ȍ����E�l���������āA����w�K��n��o���Ă����悤�Ȏp�łȂ����Ƃ͊m���ł��傤�B�Z���Ȃ́u�T���I�Ȋw�K�v�ł���A�����Ɛ��w�I�Ȍ����E�l���������āA�ߋ��Ɋw�m���ƐV�������������m�����\����������ƂƂ��ɁA��������������ɔ��W�I�ɍl����悤�Ȏq�ǂ��̎p�����҂��������̂ł��B
�@�Έ�i2024�j�́A�w�K�̓��@�Â��Ɋւ�������̏�ӂ�1�Ƃ����u���Ɍ�������̐��v������A�w�K�̌��ʐ��܂�A�w�K������t����o���̏�ӂ�1�Ƃ����u���ȂɌ�������̐��v������Əq�ׂĂ��܂��B��q�̌v�Z���K������s���q�ǂ��̎p�́u���Ɍ�������̐��v�͂���ƌ����܂����A�u���ȂɌ�������̐�������v�Ƃ͌����Ȃ��ł��傤�B�Z���Ȃɂ�����u���ȂɌ�������̐�������v��ԂƂ����̂́A��1��Ŏb��I�ɒ�`�����u�q�ǂ����w���w�I�Ȍ����E�l�����x�����Ȃ���A�K�������m���y�ыZ�\�����p���邱�Ƃ�ʂ��āA�V���Ȗ₢�����w�K�v�����Ă����Ԃł��傤�B����Z����n��o���Ă���p�Ƃ����Ă��悢�ł��傤�B
�@�܂��A�Έ�i2020�j�́u�ᔻ�I�Ɏv�l���悤�Ƃ���ԓx��w�ё����悤�Ƃ���ӎu�Ȃǂ̏o���̏�ӂ́A���犈����ʂ��Ă����q�ǂ��̂Ȃ��ɐ����č��Â��Ă������l����ω��ł���A�ړI��ڕW�Ƃ��Čf��������̂ł��v�Əq�ׂ�Ɠ����ɁA�o���̏�ӂ́A�ӎ��I�Ɏw�����邱�Ƃň��ł�����Ƃ��q�ׂĂ��܂��B
�@�����Ȃ�u�ł́A�w�T���I�Ȋw�K�x�����Ă݂܂��傤�v�ƌ������Ƃ���ŁA�q�ǂ��͉�������Ă������킩��܂���B�u�T���I�Ȋw�K�v���ł���悤�ɂȂ邽�߂ɂ́A���t���Ӑ}�I�Ɏw�����Ă������Ƃ̐ςݏd�˂��d�v�Ȃ̂ł��B
�P�������̈�Ď��ƂŐ��w�I�Ȍ����E�l�������Ӑ}�I�Ɏw������
�@6�N�u�������v�̎��H���ɁA���w�I�Ȍ����E�l�������Ӑ}�I�Ɏw�����Ă������Ƃɂ��Đ������܂��B�ŏ��Ɍ����Ă����������Ƃ́A�����������w����S�苭���ςݏd�˂Ă������Ƃ��d�v���Ƃ������Ƃł��B�����ŏЉ��q�ǂ������̎p�́A1�N�ȏ�̐ςݏd�˂̌��ʂƂ��Č��ꂽ���̂ł��B
�@�܂��A���w�I�Ȍ����E�l�������Ӑ}�I�Ɏw�����邽�߂ɂ́A��Ď��Ƃ͌������܂���B��Ď��Ƃ́A�S���̎q�ǂ��Ə������L���邽�߂ɓK�����w�K�`�ԂȂ̂ŁA�ڂ̑O�̒P���œ������鐔�w�I�Ȍ����E�l���������L���邽�߂ɁA�P���̓����ň�Ď��Ƃ��s���̂͑�Ȃ��Ƃł��B
�@�{���H��1���Ԗڂł́A�����`�ɕ��ׂ����̌����v�Z�ŋ��߂���@���l���邱�Ƃ�ʂ��āA�������̊w�K�ŏd�v�ȁA�Ɨ��ϐ��A�]���ϐ��A�萔�Ƃ��������w�I�Ȍ��������L���Ă����ƂƂ��ɁA�����������邽�߂ɂ́A�u��肪�������琔�𑝂₵�Ă݂�v�u�����c�ɕ��ׂāw�����x�Ɓw�Ⴂ�x��������v�Ƃ������A�{�P���ɂ����鐔�w�I�ȍl�����̓��������i�����I�E���W�I�ȍl���̓��������j�����L���܂����B
�ʐ^1�@�P�������̈�Ď��Ƃɂ����Đ��w�I�Ȍ������������@
�ʐ^2�@�P�������̈�Ď��Ƃɂ����Đ��w�I�Ȍ������������A
�@���ƒ��Ɏq�ǂ��������������w�I�Ȍ����i���̃N���X�ł́u���ڃ|�C���g�v�ƌĂ�ł��܂��j�́A���t���P�����ƂɌ��ꉻ����Microsoft Teams��ɂ܂Ƃ߁A���ł�������悤�ɂ��Ă��܂��B�������邱�Ƃɂ���āA����܂œ������Ă������w�I�Ȍ������q�ǂ������ł��U��Ԃ���悤�ɂ��A�������w�I�Ȍ������ӎ������Ă��܂��B
�ʐ^3�@Teams��ɒP�����Ƃɂ܂Ƃ߂�ꂽ���w�I�Ȍ���
��Ď��Ƃŋ��L�������w�I�Ȍ����E�l�������ӎ����Ȃ���T������ʊw�K
�@�Q���Ԗڂ͐��O�p�`�ɕ��ׂ����̌��̋��ߕ������ɕ\�����@���l����w�K����Ď��Ƃōs���A�R���Ԗڂ́u�~�������߂���@���A���Ƃ����g���Ď��ɕ\���܂��傤�v�u�P����3kg�̓S�̖_�̒����Əd���̊W���A���Ƃ����g���Ď��ɕ\���܂��傤�v�Ƃ���������A�ʊw�K���s���܂����B
�@���̎ʐ^�S�́A����q�ǂ����R���Ԗڂɏ������m�[�g�ł��B
�ʐ^4�@���w�I�Ȍ�����������Ă���ʊw�K���̎q�ǂ��̃m�[�g
�@���ڂ��ׂ��́A�m�[�g���������́u���ڃ|�C���g�v�Ə�����Ă��镔���ł��B���̎q�ǂ��́u�萔����������Ɨ��ϐ���]���ϐ���������B�����Z�̈Ӗ��ɂ��Ƃ����čl����i�����}�}�j�v�Ə����Ă��܂��B�P�������ŋ��L�������w�I�Ȍ������ӎ����Ȃ���w�K���Ă��邱�Ƃ��킩��܂��B���̎q�ǂ��́A�u�����ł������悤�ɍl����A�������������̂��H�v�ƍl���āA�����������W�����A���͈̔͂��L���Ă��܂����B�܂��A�w�K�̐U��Ԃ�ŁA�ʐ^5�̂悤�Ɂu���͖ʐς����߂Ă݂���!!�v�Ə����A����Ȃ锭�W�I�ȍl�@�����悤�ƍl���Ă��܂����B
�ʐ^5�@����Ȃ锭�W�I�ȍl�@�����Ă���q�ǂ��̐U��Ԃ�
�@�ʊw�K���́A�����������w�I�Ȍ����i���ڃ|�C���g�j��Teams�ɓ��e�i�ʐ^�U�Q�Ɓj���ċ��L����ƂƂ��ɁA�����������w�I�Ȍ������ӎ��ł��Ȃ������q�ǂ��́A���̓��e�����āu�����������Ƃɒ��ڂ�������̂��v�Ɨ����ł���悤�ɂ��Ă��܂��B�܂��A���t�͂��̓��e�����āA�ʐ^3�ŏЉ���P�����Ƃɓ����������w�I�Ȍ��������M������A�u�݂�ȁ����Ƃ������ڃ|�C���g�����Ă���݂������˂��v�Ǝ������p�����肵�āA���w�I�Ȍ��������L���Ă��܂��B
�ʐ^6�@�ʊw�K���Ɏq�ǂ��������������w�I�Ȍ��������e���ꂽTeams
���w�I�Ȍ������ӎ����邱�Ƃ��A�Z���Ȃɂ�����u���ȂɌ�������̐��v����Ă�
�@�ʐ^4�̃m�[�g���������q�ǂ��́A���w�I�Ȍ������ӎ����邱�ƂŁA�u����ς蓯���悤�ɖ�肪�������v�u��������A�����悤�ɏ����ł��ł��邩�ȁH�@�ʐςł��ł��邩�ȁH�v�ƍl���邱�Ƃ��ł����̂ł��B���t�Ɂu���͂�������Ȃ����v�ƌ����Ȃ��Ă��A���W�I�ɍl���邱�Ƃ��ł��Ă��܂����B���̎p�́A�u�v�Z�������Ȃ肽���v�u�e�X�g�œ_��������悤�ɂȂ肽���v�Ƃ������v���ł͂Ȃ��A�u�����Ƃ���Ȃ��Ƃ͂ł��Ȃ����ȁH�v�ƍl����A�܂��ɎZ���Ȃɂ�����u���ȂɌ�������̐��v�����ł���p�ł��B
�@�P�������ŁA�ڂ̑O�̒P���œ������鐔�w�I�Ȍ����E�l���������L���������ŁA�ʊw�K�ɂ����Ă����w�I�Ȍ������ӎ����Ċw�K��i�܂��Ă����B���X�A���̂悤�Ȋw�K�����t���ӎ��I�ɐςݏd�˂Ă������Ƃ��A�q�ǂ��̎Z���Ȃɂ�����u���ȂɌ�������̐��v����āA�u�Z���Ȃɂ�����w�T���I�Ȋw�K�x�v���s���q�ǂ�����ĂĂ������ƂɂȂ���̂ł��B
�@
�@����͂��̑����́A�P�����́u�T���I�Ȋw�K�v�̗l�q�����Љ�܂��B���y���݂ɁI
�y�Q�l���p�����z
�E�Έ�p�^�i2024�j�u�w�K�w���v�̖̂ڕW�E���e�̎������ɂ��āv�i�ߘa6�N6��10������̋���ے��A�w�K�w���y�ъw�K�]�����݂̍���Ɋւ���L���Ҍ�����i��12��j����2�Dp.16�j
�E�Έ�p�^�i2020�j�w�����̊w�Z�@�|�X�g�E�R���i�̌�����̃��f�U�C���x�i���{�W���jp.78