数学的な見方・考え方を働かせて、学習のつながりを意識し、統合的・発展的に考えて学習を進めることは、算数科における「探究的な学習」において不可欠です。しかし、単元の学習との関連性が薄くても、自分が気になったことを、とことん考える経験も貴重な時間です。今回の連載では、単元を通して働かせてきた数学的な見方をいったん置いておき、子どもが気になったことに没頭して考えた姿をご紹介します。そして、第1回で暫定的に捉えた、算数科における「探究的な学習」を捉え直します。
いったん、単元を通して働かせてきた数学的な見方を置いておく
前回、「教科に向かう主体性」を養うための「単元末の『探究的な学習』」の実践をご紹介しました。今回ご紹介する実践も、「単元末の『探究的な学習』」の実践ではあるのですが、それまで学習してきたことのつながりを意識しているというよりも、「気になったからもっとやってみたい!」 という気持ちを優先した「探究的な学習」の実践をご紹介します。ご紹介するのは、6年「比」の「単元末の『探究的な学習』」です。
まず、写真1をご覧ください。これは、「比」の単元を通して働かせてきた数学的な見方を私がTeamsにまとめたものです。

写真1 比の学習で働かせてきた数学的な見方の一覧
単元内の学習では、「今までの学習と同じように数学的な見方を働かせることができるかな?」や「もっと他の数学的な見方を働かせられるかな?」と考えて学習を進ませてきました。数学的な見方を働かせた方が、学習のつながりも意識しやすくなりますし、統合的・発展的に考えるといった数学的な考え方も働かせやすくなるからです。
数学的な見方を働かせることによって、「何のためにやっているのか」という学習の目的も自覚しやすくなります。何より、「次はこんなこともできそうだ!」と発展的に考え、自ら学習を創り出す経験がしやすくなるのです。
数学的な見方・考え方を働かせて、学習のつながりを意識し、統合的・発展的に考えて学習を進めることは、算数科における「探究的な学習」において不可欠ですが、単元に1時間ぐらいは、学習のつながりがあまり意識されなかったとしても、自分が気になったことを、とことん考える時間を設けてもよいのではないかと考えています。要するに「それって、この単元にはあまり関係ないんじゃない?」ということでも、子どもが気になったことであれば、考える時間を設けるということです。
私は、数学的な見方・考え方を働かせて、算数科の学習を創り出すことが基本だと考えています。同時に、純粋に気になったことを探究することも大切なことだと思っています。だから、もし本当に気になったことがあれば、単元で働かせてきた数学的な見方を一度置いておいて、「なんでだろう?」と思っていることを存分に考えてもらいたいと考えています。
「気になったこと」を考える子どもの姿
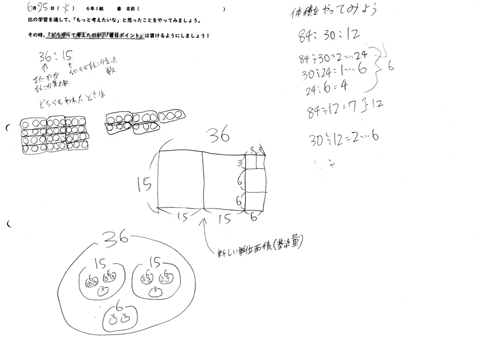
写真2は、2つの数の最大公約数の見つけ方について探究した子どものノートです。2つの数の約数の見つけ方を探究し始めたのは、この子どもが「18:27を簡単な比にする時は、27−18をすれば、わる数が見つかる」という話をまわりの子どもとしていたのを私が聞いて、「本当に?」と声かけしたことがきっかけでした。
この子どもは、「比の数の差が、比を簡単にするときの最大公約数になる」という、少しあやふやな先行知識をもっていました。それを聞いて、私から「どんな数の比でも使えるの?」と問いかけたところ、36:15ではどうなるのかを考え始めたのです。
探究が始まると、あまりにも悩むので、まわりの子どもが寄ってきて、「何考えているの?」と興味をもちはじめ、一緒に考えていました。
図をかいたり、議論したりしていたのですが、なかなか解決の糸口が見つからなかったので、私から「ユーグリッドの互除法って知っている?」と声をかけました(ここではユーグリッドの互除法の解説は割愛します)。「知らない」というので、「インターネットで調べてみるといいよ」と声をかけて、また他の子どもの所に移動しました。
写真2 約数の見つけ方について探究した子どものノート
数分後、この子どものところに戻ってみると、ノートの真ん中に長方形の図がかかれていて、ユーグリッドの互除法について考えている跡が残されていました。感心したのは、右側の「体積をやってみよう」と書かれた部分です。この子どもは、ユーグリッドの互除法の理解で終わらず、「ユーグリッドの互除法は、3つの比でも同じようにできるのか?」と考えていました。時間がなくて、十分な理解まで到達していなかったようですが、これこそ算数科における「探究的な学習」をする姿だなと感じました。
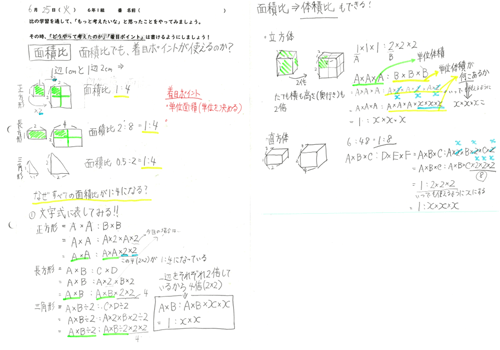
他にも、自分で気になったことを探究する子どもがいました。写真3のノートを書いた子どもは、面積比や体積比について考えていました。きっと、だれかが面積比や体積比を知っていて、それを聞いたことをきっかけに考え始めたのだと思います。
写真3 面積比や体積比について探究した子どものノート
学級の中には、先行知識をもっている子どももいます。知識をもっていること自体はまったく問題ありません。むしろ、もっている知識を自然と言える環境を整えることが健全だと思います。でも、ただ知っているだけでなく、「どうしてそうなるのかな?」と考えることが大事であり、「なぜ?」を考える「探究的な学習」になってほしいと考えています。
教師は、「みんなが解けるようになること」に目を向けがちです。それは、公教育として正しいことだと思います。でも、すでにいろいろと知っている子ども、算数が得意な子どもにも、他の子どもと同じように算数科における「探究的な学習」を楽しんでもらえる環境は整えたいと考えています。
算数科における「探究的な学習」の捉えを再考する
今回、単元を通して働かせてきた数学的な見方を働かせることをあまり意識せず、「気になったからもっとやってみたい!」という気持ちを優先した「探究的な学習」を紹介しました。
数学的な見方を働かせた方が、学習のつながりも意識しやすくなりますし、統合的・発展的に考えるといった数学的な考え方も働かせやすくなります。ですから、基本的には、数学的な見方・考え方を働かせながら学習を進めていく方がよいと考えています。
しかし、数学的な見方・考え方を働かせることだけが「探究的な学び」としてしまうと、「教科に向かう主体性」をしぼませてしまう恐れもあるのではないかと考えています。ですから、子どもが「もっとやってみたい!」と思ったことがあれば、単元の学習から少し脱線した内容であったとしても、少し時間を設けて、没頭させることも必要だと考えています。
以上のことを踏まえ、第1回で暫定的に捉えた算数科における「探究的な学習」の捉えを、次にように加筆・修正したいと思います。
「子どもが『数学的な見方・考え方』を働かせながら、習得した知識及び技能を活用すること 等を通して、新たな問いをもつ学び」
加筆したのは「等」という言葉です。この「等」の中に、数学的な見方・考え方を働かせること以外でも、子どもなりに新たな問いをもつ学習を算数科における「探究的な学習」に含めていきたいという意図を込めました。
しかし、写真2や写真3の子どもは、自分で発展的に考えており、数学的な考え方を働かせていることがわかります。こういった姿は、日々の学習において、数学的な見方・考え方を働かせてきた積み重ねによるものだということを忘れてはいけません。