- �Z���Ȃ̒T���I�Ȋw�K
- �Z���E���w
- �R�����g(0)
�@�u�T���I�Ȋw�K�v�Ƃ����ƁA�q�ǂ��Ɋw�т��ς˂���搶�͌���邾���A�Ƃ����C���[�W������̂ł͂Ȃ��ł��傤���B�m���ɁA�q�ǂ��̊w�т����������~�߂邱�Ƃ͂��Ȃ������悢�ł��傤�B�������A�u�����ďI���v�́u�T���I�Ȋw�K�v�ɂ��Ȃ����߂ɂ́A�q�ǂ��̊w�K�̗l�q�������A���w�I�Ȍ����E�l�����������悤�Ȑ����������Ă������Ƃ���ł��B
�@�܂��A�����������Ƃ��ł��Ȃ��q�ǂ���������A�ꏏ�ɍl������A�������肵�Ȃ���A�u�T���I�Ȋw�K�v���n�߂���悤�ɂ��邱�Ƃ��A���t�̑�Ȗ����ɂȂ�܂��B
�b�������l�Ɏ��R�ɘb�������z��
�@�����ɁA�����̎��ƂŁu���R�ɗ��������āA����ɕ����ɍs���Ă�������v�Ǝq�ǂ��ɐ��������Ă݂Ă��������B�����Ɏq�ǂ������������n�߂���A���łɁu���R�ɂ���ɂł������ɍs���Ă����v�Ƃ����w�K���͐����Ă��܂��B
�@�������A�����̊w���ł́A���܂�q�ǂ��͓����Ȃ��Ǝv���܂��B�Ȃ��Ȃ�A�u�w�K�͎����̐Ȃō����čs�����̂��v�Ƃ����Œ�ϔO���q�ǂ��������Ă��邩��ł��B�������́A�u�ꏏ�ɘb������A�l�����肷�鑊��⎞�Ԃ́A�搶�����߂���̂��v�Ƃ����Œ�ϔO�������Ă��邩������܂���B
�@���N�������Ď����̔��f�œ����Ȃ����Ƃ�������Ă��Ă�����A�����Ȃ����Ƃ����ʂł��B���̏�Ԃ������ɑŊJ���邱�Ƃ͓���ł����A������������Ă����̂ł��B�Ⴆ�A���ꂩ���������낢���Ƃ����Ă����Ƃ��A�u�������������낢���Ƃ����Ă����I�v�ƑS�̂ɐ�����������A��������悤�Ƒ����̎q�ǂ����W�܂��Ă���Ǝv���܂��B���̂Ƃ��A�����������ē������q�ǂ��ɑ��āu�����Œm�肽���Ǝv�������Ƃ��A�����̐Ȃ��瓮���Č��ɍs���Ă��炵���I�v�Ƃ����������������Ă����̂ł��B���������������𐔂��������Ă����ƁA����Ƙb�������l�̂Ƃ���֕����ɍs���q�ǂ��������Ă����܂��B
�@�������A�܂��ׂ͗̐l�A�܂��̐l�Ƙb���Ă��瓮���悤�ɂ��܂��B�������Ȃ��ƁA����̐l�Ƃ���b���Ă��܂��悤�ɂȂ��Ă��܂����ꂪ���邩��ł��B
�u�T���I�Ȋw�K�v�̍ۂ̋��t�̓����Ɛ�����
�u�T���I�Ȋw�K�v�̍ۂ̋��t�̓����̃C���[�W�}
�@��}�́A�u�T���I�Ȋw�K�v�̍ۂ̋��t�̓����̃C���[�W�}�ł��B�w���̒��ɂ́A�l�ŒT�����Ă���q�ǂ����������܂����A�����́A�����Ŗ��������Ă܂��̐l�����Ɖ������̋��L�Ȃǂ�������A���������Ď����̋��������邱�Ƃ�����Ă���l�������m��2�`4�����x�̃O���[�v�������Ċw�K���n�߂܂��B�������A�����������A�����̐Ȃ̂܂��̐l�����ƈꏏ�Ɋw�K��i�߂�q�ǂ����������܂��B
�@���t�́A�l�Ŋw�K���Ă���q�ǂ���e�O���[�v�����g��ł��邱�Ƃ�c�����邽�߂ɁA���邮�鋳���̒���������A���������܂��B�������̃p�^�[���́A��Ɉȉ���3�ł��B
�@���͉������H
�A�ǂ�Ȓ��ڃ|�C���g�i���w�I�Ȍ����j���g�����H
�B���͂ǂ�Ȃ��Ƃł������H
�@�u�@���͉������H�v�́A�������i1��ڂ͑S�����ʂ̖��ł���Ɠ����ɁA�S���������ł���悤�ɂȂ��Ă��炢�������B�����́A���ȏ��ʂ�̖��j�����������ǂ����̊m�F�ł��B�ł��Ȃ��q�ǂ���������A�����ɑΉ����܂��B��l��l�Ή����Ă���Ǝ��Ԃ��������Ă��܂��̂ŁA�u�w������Ƃ킩��Ȃ��č����Ă����x���Ă����l�́A���̑O�ɂ����Łv�Ȃǂ̐����������t���炵�āA�q�ǂ����W�߂ĉ�����܂��B
�@�u�A�ǂ�Ȓ��ڃ|�C���g�i���w�I�Ȍ����j���g�����H�v�́A�������������ďI���ɂ����A���w�I�Ȍ��������邱�Ƃ��ł������ǂ����̊m�F�ł��B�q�ǂ��͂ǂ����Ă��u�������ƂŐ���t�v�ɂȂ�܂��B�����ŁA�����I�������ɁA�q�ǂ��������������w�I�Ȍ��������o�����A���K�Ƃ̂Ȃ�����ӎ�������̂ł��B���w�I�Ȍ���������͎̂q�ǂ��ŁA���t�͎q�ǂ��������������w�I�Ȍ��������o�����������S���Ă���ƍl���Ă��܂��B
�@�u�B���͂ǂ�Ȃ��Ƃł������H�v�́A���W�I�ɍl�@���邱�Ƃ𑣂��������ł��B�����琔�w�I�Ȍ�������������ꂽ�Ƃ��Ă��A���t����^����ꂽ�����������Ƃ���Ŏ~�܂��Ă��܂��ẮA����w�K��n��o���Ă���Ƃ͌����܂���B�����ŁA�u���͂ǂ�Ȃ��Ƃł������H�v�Ɣ��W�I�ɍl�@���邱�Ƃ𑣂��̂ł��B
��肪�����Ȃ������q�ǂ��ւ̑Ή�
�@�����Ŗ�肪�����Ȃ��q�ǂ��́A2�p�^�[���ɕ�����܂��B
�@1�́A�܂��̎q�ǂ��ɉ��������q�ǂ��ł��B���������s��������q�ǂ��́A�����������������Ȃ��Ă����͂���܂���B
�@����1�́A�킩��Ȃ��Ȃ��Ď~�܂��Ă��܂��A�������́A�Ԉ���������������Ă��Ă��C�Â��Ȃ��A�Ƃ����q�ǂ��ł��B���������q�ǂ��́A�u�����łȂ�Ƃ����悤�v�Ǝv���߂��Ă��܂��̂ŁA�����琺��������悤�ɂ��Ă��܂��B
�@�܂��A�q�ǂ����ǂ�ȉ����������Ă���̂��A�����ԗl�q�������܂��B�����āA�킩��Ȃ��Ȃ��Ă��邩�A�Ԉ���������������Ă���ꍇ�́A�u�������H�v�Ɛ��������܂��B����ƁA���������u���`��v�ƍ������悤�ȕԎ������邱�Ƃ������ł��B���̂Ƃ��́u���Ⴀ�A�搶�ƈꏏ�ɂ���Ă݂悤�v�Ɛ���������Ɠ����ɁA�u�����Ȃ��č����Ă���l��������W�܂��āv�ƃN���X�S�̂ɐ��������܂��B��������ƁA4�`5���̎q�ǂ����W�܂��Ă��܂��B
�@�����ł̃|�C���g�́A�A�u�q�ǂ��ɐ���������v�Ƃ������Ƃł��B���낢��Ȏq�ǂ�������̂ŁA�ꏏ�ɍl���Ȃ�����������Ă��悢�ł����A�܂��͐搶����������������Ă��悢�Ǝv���܂��B�������A�u�����ďI���v�ɂ��Ȃ��Ƃ������Ƃł��B
�@��l���q�ǂ��������ŁA�l�͐������Ɓu�킩��������v�ɂȂ�܂��B�������A���ۂɂ���Ă݂�Ɓu������A������Ăǂ����낤�H�v�ƂȂ邱�Ƃ������Ǝv���܂��B������A�A�ꏏ�ɍl������A�搶�����������肵����A�u���Ⴀ�A���̂��Ƃ�������x�������Ă݂āv�Ɛ��������āA�q�ǂ��ɐ����������̂ł��B
�@�ʐ^1�́A6�N���̉~�̖ʐς̊��p�̊w�K�ŁA�悭���郉�O�r�[�{�[���^�̖ʐς̋��ߕ����ʊw�K�ōl�����ۂ̃m�[�g�ł��B
�@���̎q�ǂ��́A�ʐς̊w�K�̍ۂɂ́u�ʐς����߂���`�ɂ���v�Ƃ������w�I�Ȍ��������邱�Ƃ͈ӎ��ł��Ă��܂����B�������A�ǂ�Ȍ`�ɕό`����悢�����v�����Ȃ��č����Ă��܂����B���l�̎q�ǂ������l�������̂ŁA���������āA���̎q�ǂ��̊��̂܂��ɏW�߂܂����B
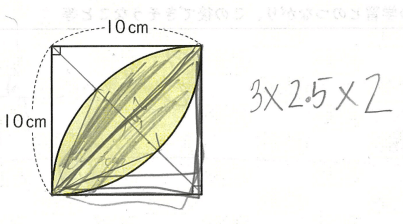
�ʐ^1�@�ʊw�K���Ɏ��͂ʼn����ł��Ȃ������q�ǂ��������Ă����m�[�g
�@�����ŁA1/4�~���璼�p�O�p�`�̖ʐς��Ђ��āA���O�r�[�{�[���^�̔����̖ʐς��o���āA�����2�{����Ƃ������ߕ���������܂����B
�@�u(10�~10�~3.14��4�|10�~10��2)�~2�v
�@�����Ə�̂悤�ɂȂ�܂��B���̉�@����������������A�q�ǂ��Ɂu���Ⴀ�A���̉������A����1��������Ă݂āv�ƌ����āA�������Ă��炢�܂����B���̍ۂ��A���w�I�Ȍ������ӎ��ł���悤�ɁA������u�ʐς����߂���`�ɂ�����Ē��ڃ|�C���g�i���w�I�Ȍ����j�͎g�����H�v�Ɩ₢�A1/4�~��O�p�`�̖ʐς����߂�ۂɓ������Ă��邱�Ƃ����o�������Ă����܂����B
�@�����܂ŏI���A���Ƃ͊e���̐Ȃɖ߂��āA�܂��̎q�ǂ��ƈꏏ�ɁA�Ⴄ���������l������A���W�������肷�邱�Ƃ��ł��܂��B
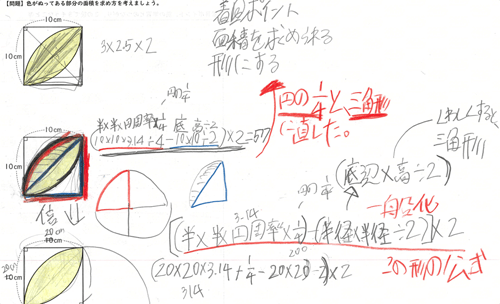
�@���Ȃ݂ɁA�ʐ^�P�̃m�[�g���������q�ǂ��́A�w�K�̌㔼�ł́A�܂��̎q�ǂ��ƈꏏ�ɁA���O�r�[�{�[���^�̖ʐς̌������l���Ă��܂����i�ʐ^�Q�Q�Ɓj�B�܂��ɁA�Z���Ȃɂ�����u�T���I�Ȋw�K�v�����Ă��܂����B
�ʐ^2�@���O�r�[�{�[���^�̖ʐς̌������l�����m�[�g
�@���̎q�ǂ����������̂́A�����`��1�ӂ̒�����20�p�̏ꍇ�ł��m���߂āA��ʉ���}���Ă���Ƃ���ł��B
�@�����A����1��ڂ̉������������Ȃ���A�����܂Łu�T���I�Ȋw�K�v�����邱�Ƃ͂ł��Ȃ�������������܂���B�������A�u��肪�����Ȃ��q�ǂ��́A�w�T���I�Ȋw�K�x�Ȃǂł��Ȃ��v�ƍl����̂͑��v�ł��B�A�����Ŗ�肪�����Ȃ��Ă��A���������킩��A�u�������灛�����ł��邩������Ȃ��I�v�ƍl������q�ǂ��͂��������̂ł��B