
- �Z���M�����ƂÂ���
- �Z���E���w
- �R�����g(1)
�M�����ƂÂ���̃|�C���g
- �s�v�c�Ȃ������Ŏq�ǂ��̖₢�������o��
- ���ʐ���Nj������b�������̏��ݒ肷��
- ��̕��̑���A���Ƃ̊֘A�t���ł������ɔ���
1�@�s�v�c�Ȃ������Ŏq�ǂ��̖₢�������o��
�@�u�����Z�̂��܂�v�̓������Ƃ̖`���ŁA�u�搶�Ƒ����肢�����悤�v�Ǝq�ǂ������ɓ��������܂��B
�s�@�搶�Ƒ����肢�����܂��傤�B�菇�ɏ]���āA�搶�Ƃ̑�����\���}�[�N�����肵�܂��傤�B�F�����Ƒ��k����������l�Ń}�[�N�����肵�Ă��������B
- �菇�@
- �D����2�����̐��Ɏv�������ׂ܂�
- �菇�A
- �@�̐��|�@�̐��̈�̈ʂ̐�
- �菇�B
- �A�̐��|�@�̐��̏\�̈ʂ̐�
- �菇�C
- �B�̐��ɑΉ�����}�[�N�����̕\����I�т܂�
| 0 �� |
10 ☂ |
20 ☁ |
30 ☀ |
40 ☃ |
50 ☂ |
60 �� |
70 �~ |
80 �� |
90 ♡ |
| 1 ☀ |
11 �� |
21 �� |
31 �� |
41 ☁ |
51 �� |
61 �� |
71 �� |
81 ♡ |
91 �� |
| 2 �� |
12 ☃ |
22 �� |
32 ☁ |
42 �� |
52 ☁ |
62 ☀ |
72 ♡ |
82 ☁ |
92 �� |
| 3 ☁ |
13 �� |
23 ☀ |
33 ☂ |
43 ☃ |
53 �� |
63 ♡ |
73 ☂ |
83 �� |
93 ☂ |
| 4 �~ |
14 �� |
24 �� |
34 �� |
44 �� |
54 ♡ |
64 �~ |
74 �~ |
84 �� |
94 ☃ |
| 5 �� |
15 �~ |
25 �� |
35 �� |
45 ♡ |
55 ☀ |
65 �� |
75 �� |
85 �~ |
95 ☀ |
| 6 ☂ |
16 ☀ |
26 ☃ |
36 ♡ |
46 �~ |
56 �� |
66 ☂ |
76 ☀ |
86 ☀ |
96 �� |
| 7 �� |
17 �� |
27 ♡ |
37 �~ |
47 �� |
57 �� |
67 ☃ |
77 �� |
87 �� |
97 �~ |
| 8 ☃ |
18 ♡ |
28 ☂ |
38 �� |
48 ☀ |
58 ☂ |
68 ☁ |
78 ☁ |
88 ☁ |
98 �� |
| 9 ♡ |
19 ☁ |
29 �~ |
39 ☃ |
49 �� |
59 �~ |
69 �� |
79 �� |
89 ☂ |
99 ♡ |
�@�q�ǂ��������}�[�N�����肵����A��l�����O�ɌĂсA���̎q�ɂ킩��Ȃ��悤�ɁA���̎q�̃}�[�N��I�������܂��B
�s�@�ł́A�}�[�N�Ă܂��B�搶�Ƃ̑����́c�A♡�ł���H
�@������J��Ԃ��A�����̃}�[�N�����X�ɓI�������Ă����܂��B
2�@���ʐ���Nj�����b�������̏��ݒ肷��
�@���́A���̑����肢�ł́A�ǂ��2�����̐���I��ł��菇�B�ł�9�̔{���ɂȂ�A�}�[�N��♡�ɂȂ�܂��B
�@�搶�����X�Ƀ}�[�N��I�����������Ƃɋ^���������q�ǂ������́A�܂��̗F�����̃}�[�N���������m�F�������A�S����♡�ł��邱�ƂɋC�t���܂��B
�b�@������H�@�݂��♡�����I
�b�@�ł��A�@�őI���̓o���o���Ȃ̂ɁA�Ȃ�ł݂��♡�ɂȂ�́H
�c
�@��̂��Ƃ肩��킩��Ƃ���A���ʐ���Nj�����Ƃ����s�ׂ́A������������s�ׂ��̂��̂ŁA�q�ǂ�����̓I�ɋ��ʐ��ɋC�t�����Ƃ���悤�Șb�������̏��ݒ肷�邱�Ƃ���ł��B
3�@��̕��̑���A���Ƃ̊֘A�t���ł������ɔ���
�@�q�ǂ��������v�Z�̎菇�ɔ閧������Ɗ��Â����Ƃ���ŁA��̓I�Ȑ���1�����A�u���b�N��p���Ď菇���Č�����悤�ɑ����܂��B
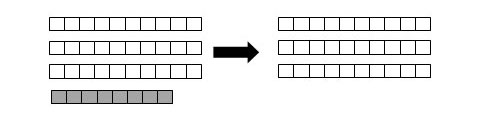

�@���̂悤�ɁA����ʂ���̕���}�ŕ\���A���삷�邱�Ƃł������������Ă���Ƃ����o���A�����āA��������Ɗ֘A�t���邱�Ƃł����������炩�ɂȂ�Ƃ����o���́A�������͂��͂����ނ����Ŕ��ɏd�v�ł��B
-
- 1
- ����܂Ȃ�
- 2013/8/10 6:19:30
���킢���搶�ł��ĂˁB
