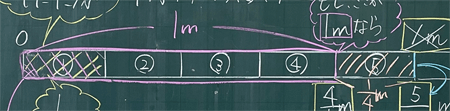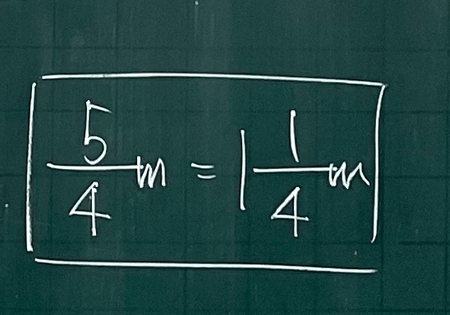- とっておき算数授業
- 算数・数学
本時のねらい
真分数の意味を理解するとともに、1より大きい量の表し方を考え、2通りの表し方(帯分数と仮分数)を理解する。
板書
板書のとっておきポイント
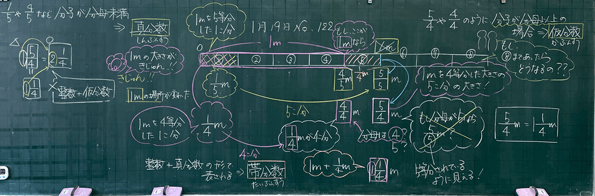
- 話合いのメインとなる図を黒板の中心に据え、1mを5等分したときと4等分したときの考えを比較するように意識して板書した。
授業の流れ
1考えのずれから問いをもつ(15分)
1mを5等分したテープ図を板書する。
この1mは、何分の何mと表現すればよいかな?
簡単だよ。
5/5mでしょ。
どうして5/5mと言えるのかな?
1mを5等分したうちの5個分の長さだからだよ。
そうそう。1mを5等分した1個分が1/5mでしょ。その5個分だから5/5mだよ。
なるほど。では、もし、さっき4/5mだったところが1mだったとしたら、このテープは何分の何mになるのかな?
えっ?それだったら、5/4m?
何で?5/5mじゃないの?
どっちだろう?
2単位分数の大きさに着目して解決する(20分)
それぞれの立場の意見を聞いてみましょう。まず5/5mの方から。
テープ全体の長さは変わってないでしょ?だから5/5mだと思うよ。
さっきと同じで1個分は1/5mだから、その5個分だったら5/5mになるんじゃないの?
なるほど。確かに言われてみればそんな感じがしますね。
違うよ。今回は1mの場所が変わったでしょ。それだと4/5m=1mとなってしまうよ。
さっきまでは1mが5等分されていたけど、今度はさっきまで4/5mだったところが1mになっているでしょ。だから、1mが4等分されたことになっているんだよ。
あ〜何となく言いたいことが分かってきた気がする。
つまり、さっきまで4/5mだったところが4/4mになったってことだよ。
そっか。1mの場所が変わって、1mが4等分される形になったから1mを4等分したうちの4個分で4/4mか。
1mの大きさが基準ってことだね。騙されるところだった。
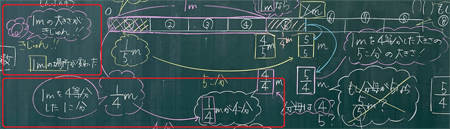
ということは、このテープは1mが4等分された5個分ということになるから5/4mの方だね。
何だかモヤモヤがスッキリに変わってきた人が多いようですね。このテープが5/5mではなく、5/4mであるという理由についてペアで確認してからノートに整理しましょう。
3真分数と仮分数、帯分数について知る(10分)
1/5や4/5のように、分子が分母より小さい分数のことを真分数と言います。逆に、5/4や4/4のように分子が分母と等しいか大きい分数のことを仮分数と言います。
真分数と仮分数か。
真と仮で反対だね。分かりやすい。
最後に確認です。5/4mってどんな大きさ?と問われたら何と答えますか?
1/4mが5個集まった長さ。
1mよりも1/4m大きい長さ。
どちらも正しい表現ですね。1mよりも1/4m大きいということを表現するために、帯分数というものがあります。
授業終末の振り返り記述に「もし、テープが(5)の部分で終わりではなく、(8)まであったとしたら、5/4mの部分は5/8mとなるのか?」ということを書いていた人が2人いた。この新たな問いをもとに、次時は、量分数と割合分数の違いを考えさせる1時間にした。子どもの熱心な追究から少し散らかってしまって見づらいが、下の写真が次時の板書である。
授業のとっておきポイント
板書されたテープの長さは変わらないが、1mの位置が変わったら…と仮定することで表現される大きさも変わってくるという場面を問題にした。
今回子どもたちが活発に議論していたのは、「1つ分の大きさ」すなわち単位分数の大きさについてである。「1mの場所が変わっているから。」「1mが基準だ。」「1つ分は1/4mだ。」などというように、見た目上の分けられた数(テープ全体が5等分されていること)に惑わされることなく、1mを何等分しているのかということに着目することを目指した授業を考えた。
おそらく全員が5/5mだという誤答に流れることはないとは思うが、もしそうなってしまった場合には、子どもも発言していたが、「4/5m=1m」という状態を提示したり、1mの位置をどんどん短く仮定していったりすることで揺さぶりを掛けることを想定していた。
また、最後に2人の子どもが振り返りに記述していた「もし、テープが(5)の部分で終わりではなく、(8)まであったとしたら、5/4mの部分は5/8mとなるのか?」という内容もおおよそ想定していた。量分数というものへの理解が十分でないことと、分数を割合で捉える視点が生まれているということであると考える。子どもの分数に対する捉え方を丁寧に扱いながら、分数の様々な表し方を学んでいくことが大切だと思っている。