板書王のとっておき算数授業（4）
一番小さい答えはいくつ？きまり発見を楽しみながら習熟を図ろう！
3年「たし算とひき算（3けたの筆算）」（11／14時間）
2020/9/15 掲載
- とっておき算数授業
- 算数・数学
本時のねらい
答えが一番小さくなるひき算の式を考えることを通して、3けたのひき算の習熟を図る。
板書
板書のとっておきポイント
- （2けた）−（2けた）、（3けた）−（3けた）ともに、筆算を比べられるように横に並べ、子どもがきまりに気付きやすくする。
- 掲示用の筆算シートを用いることで、子どもの気付きや発言に応じて並び替えたり移動させたりできるようにする。
授業の流れ
1（2けた）−（2けた）の計算を考える（15分）
まず（2けた）−（2けた）の差が最小になる計算を考えさせる。
1〜4までの数を□に入れて、答えが一番小さくなる筆算を作りましょう。答えをできるだけ小さくするには、引かれる数と引く数の差はどうなればいいかな？
小さくなるってことだ。
2つの数が近い方がいいね。
では、□に数字を入れてできるだけ小さい答えを作ってみよう。
（3分程度自力思考の時間をとる）
できた式と答えを紹介してください。
23−14＝9
私も9だけど、式が違う。41−32＝9
もっと小さくなったよ。31−24＝7
どうやら、7が一番小さい答えのようですね。みんなは、できるだけ答えが小さくなるように、引かれる数と引く数を考えたと思うんだけど、十の位と一の位、どっちを先に考えた？
十の位と一の位でそれぞれ挙手させる。十の位（18人）、一の位（11人）
十の位という人が多いけど、どうしてかな？
だって、答えを小さくするためには、十の位が同じだったら0でしょ？
でも今回は、同じ数は使えないから、差が1になるようにしないと。
あっ！本当だ！
3つ（の式）とも十の位の差が1になっている。
でも、一の位も考えないと！くり下がりがないと答えが小さくならないから、引かれる数の方は小さい数を入れて、引く数は大きい数が入るようにするといいと思う。
今のAさんの言ったこと聞き取った？気持ちが分かるかな？
たとえば、42-31だと十の位の差は1だけど、一の位が2−1でくり下がりがないから答えが小さくならないですよね？だから41−32と、1と2の小さい方の1を引かれる数にして大きい方の2を引く数にするといいってこと。
一番小さい答えを出すポイントが見えた気がする。
計算が比較的簡単な（2けた）−（2けた）を先に扱い、差を最小にする際のポイントとして、十の位（一番大きい位）に着目させた。一の位に着目したという子にどうしてそう考えたのかを問うことで、引かれる数と引く数にそれぞれどのような数字を入れれば良いかという話へと展開されることが期待できる。ここで得た考え方は（3けた）−（3けた）の解決の際のヒントとなる。
2 （3けた）−（3けた）の計算を考える（20分）
次に（3けた）−（3けた）の差が最小になる計算を考えさせる。
2けたは解決できたね。次は何を考えたい？
3けただとどうなるのか調べたい。
1〜4の数字を他の数字に変えたい。
今回は、3けたにして考えてみようか。1〜6の数字を入れて答えが一番小さくなる筆算を作りましょう。まずは何の位から考えるといいかな？
百の位。
答えをできるだけ小さくするために、百の位に入る数字はどのようなペアが考えられる？
さっきみたいに差が1になればいいから…1と2、3と4、5と6。
2と3、4と5もできるよ。
では、□に数字を入れてできるだけ小さい答えを作ってみよう。
5分程度自力思考の時間をとり、子どもが考えた式を紙に書かせて黒板に貼る。
今度は、47が一番小さいみたいだね。
今回も同じ答えのペアがあるね。49と69。
おもしろい！また一の位が7と9しかないよ。
一番小さい答えの一の位はまた7だね。
ということは4けただったら…
百の位に入る数のペアを引き出してから自力思考に入ることで、考えが拡散しすぎず、自力でも考えられる子が多くなる。2けたのときの考えを生かして3けたを解決する姿を価値付けていきたい。
また、「一番小さい答えの引かれる数と引く数を位ごとに見て、足すとどの位も7になる（2けたのときは5）」というきまりに気付く子も出てくるかもしれない。その場合は時間を見て扱ってもいいだろう。ちなみに4けたのときは9になる。
3 （4けた）−（4けた）の計算を考える（10分）
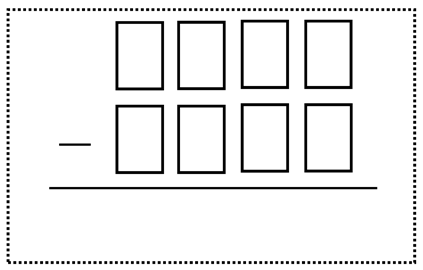
最後に（4けた）−（4けた）の差が最小になる計算を考えさせる。
4けたのことを考えている人がいてすごいね。もし（4けた）−（4けた）で1〜8までの数字を入れるとしたら、みんななら千の位にいくつを入れる？
今回もたくさんペアがあるよね。
たぶん答えが一番小さくなるのは、4と5のペアだよ。
どうして分かるの？
だって2けたのときや3けたのときにも真ん中だったから…。
答えの一の位も予想できそうだよね。先ほどの千の位に入れるペアと答えの一の位の数を、2けたや3けたのときの考えをもとに予想してノートに書きましょう。そしてその理由も書きましょう（振り返り）。
5分程度振り返りを記述する時間をとる。
今回の問題をさらに発展させるとしたら、みんなならどうする？
けた数を大きくする。
入れる数字を変えてみる。
ぜひ自学で取り組んでみてください。
最後に発展させて考える自学への意欲付けとして、4けたの場合を実際に確かめたり、数値を変えてみたりといった選択肢を出させるということは、効果的である。
授業のとっておきポイント
一番小さい答えになる計算を考える中で、いつの間にか少しずつきまりが見えてくる。見つけたきまりが他の場合にも適用できるかを考えるためにさらに計算をするというサイクルが生まれる。くり下がりのあるひき算の筆算を一定数計算することになるので、習熟を図る段階では、このように計算の中にきまりを仕込んだり、ゲーム性をもたせてみたりすると楽しく学習できる子が増える。
今回は、答えを小さくするためのポイント（着眼点）を自力思考前に共有し、全体の学びを揃えながら進めていくことを意識した。
（構成：中野）
コメントの受付は終了しました。
